
分析 (I)由题意可得2a=4$\sqrt{2}$,解得a.由点A是椭圆E的右顶点,直线BC过原点O,点B在第一象限,且|BC|=2|AB|,可得|BO|=|AB|,
又$cos∠ABC=\frac{1}{5}$,|OA|=a=2$\sqrt{2}$,利用余弦定理解得|BO|.可得B$(\sqrt{2},\sqrt{3})$,代入椭圆方程即可得出.
(II)设M(x1,y1),N(x2,y2),设直线L的方程为:y=kx+m.与椭圆方程联立化为(1+2k2)x2+4kmx+2m2-8=0,△>0,化为8k2+4>m2.利用根与系数的关系可得则|MN|=$\sqrt{(1+{k}^{2})[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$.由直线l与圆x2+y2=1相切,可得$\frac{|m|}{\sqrt{1+{k}^{2}}}$=1,化为m2=1+k2,利用S△MON=$\frac{1}{2}$|MN|,通过换元再利用二次函数的单调性即可得出.本题考查了椭圆的标准方程及其性质、直线与圆相切的性质、一元二次方程的根与系数的关系、弦长公式、点到直线的距离公式、三角形面积计算公式、二次函数的单调性,考查了推理能力与计算能力,属于难题.
解答 解:(I)∵2a=4$\sqrt{2}$,∴a=2$\sqrt{2}$.
∵点A是椭圆E的右顶点,直线BC过原点O,点B在第一象限,且|BC|=2|AB|,
∴|BO|=|AB|,
∵$cos∠ABC=\frac{1}{5}$,|OA|=a=2$\sqrt{2}$,
∴|OA|2=|BO|2+|AB|2-2|BO||AB|cos∠ABO,
∴8=2|BO|2$(1-\frac{1}{5})$,解得|BO|=$\sqrt{5}$.
∴B$(\sqrt{2},\sqrt{3})$,代入椭圆方程可得:$\frac{2}{8}+\frac{3}{{b}^{2}}$=1=1,解得b2=4.
∴椭圆E的方程为$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{4}$=1.
(II)设M(x1,y1),N(x2,y2),设直线l的方程为:y=kx+m.
联立$\left\{\begin{array}{l}{y=kx+m}\\{{x}^{2}+2{y}^{2}=8}\end{array}\right.$,化为(1+2k2)x2+4kmx+2m2-8=0,
∵直线l与椭圆相交于不同的两点,∴△>0,化为8k2+4>m2.
∴x1+x2=$\frac{-4km}{1+2{k}^{2}}$,x1x2=$\frac{2{m}^{2}-8}{1+2{k}^{2}}$,
则|MN|=$\sqrt{(1+{k}^{2})[({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}]}$=$\sqrt{1+{k}^{2}}$$\sqrt{(-\frac{4km}{1+2{k}^{2}})^{2}-4×\frac{2{m}^{2}-8}{1+2{k}^{2}}}$=$\frac{2\sqrt{2}\sqrt{1+{k}^{2}}\sqrt{8{k}^{2}-{m}^{2}+4}}{1+2{k}^{2}}$,
∵直线l与圆x2+y2=1相切,∴$\frac{|m|}{\sqrt{1+{k}^{2}}}$=1,化为m2=1+k2,
∴|MN|=$\frac{2\sqrt{2}\sqrt{1+{k}^{2}}\sqrt{7{k}^{2}+3}}{1+2{k}^{2}}$,
则S△MON=$\frac{1}{2}$|MN|×1=$\frac{\sqrt{2}\sqrt{1+{k}^{2}}\sqrt{7{k}^{2}+3}}{1+2{k}^{2}}$,
令1+2k2=t≥1,则k2=$\frac{t-1}{2}$代入上式可得:$\frac{\sqrt{2}}{2}\sqrt{-(\frac{1}{t}-3)^{2}+16}$,
∵t≥1,∴$0<\frac{1}{t}≤1$,∴$\frac{\sqrt{14}}{2}$<S△MON≤$\sqrt{6}$.
即△MON的面积的取值范围是$(\frac{\sqrt{14}}{2},\sqrt{6}]$.
点评 本题考查了椭圆的标准方程及其性质、直线与圆相切的性质、一元二次方程的根与系数的关系、弦长公式、点到直线的距离公式、三角形面积计算公式、二次函数的单调性,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
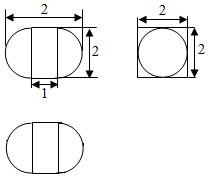
| A. | $4+\frac{2π}{3}$ | B. | $8+\frac{2π}{3}$ | C. | $4+\frac{4π}{3}$ | D. | $6+\frac{4π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{12}$ | B. | $\frac{5}{12}$ | C. | $\frac{1}{3}+ln2$ | D. | $\frac{1}{6}+ln2$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
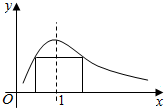 一矩形的一边在x轴上,另两个顶点在函数y=$\frac{2x}{1+{x}^{2}}$(x>0)的图象上,如图,则此矩形绕x轴旋转而成的几何体的体积的最大值是( )
一矩形的一边在x轴上,另两个顶点在函数y=$\frac{2x}{1+{x}^{2}}$(x>0)的图象上,如图,则此矩形绕x轴旋转而成的几何体的体积的最大值是( )| A. | π | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com