
分析 根据函数解析式得出$\underset{lim}{x→{1}^{-}}$f(x),$\underset{lim}{x→{1}^{+}}$f(x),判断相等与否即可判断极限是否存在.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{3-x,x≥1}\\{2x+1,x<1}\end{array}\right.$,
∴$\underset{lim}{x→{1}^{-}}$f(x)=2×1+1=3,$\underset{lim}{x→{1}^{+}}$f(x)=3-1=2,
∴$\underset{lim}{x→{1}^{-}}$f(x)≠$\underset{lim}{x→{1}^{+}}$f(x),
∴函数f(x)在点x=1的极限不存在
点评 本题简单的考察了极限的概念,极限的思想,关键利用左极限,右极限与在点的极限的关系.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{25}{4}$ | B. | $\frac{49}{9}$ | C. | $\frac{144}{25}$ | D. | $\frac{225}{49}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
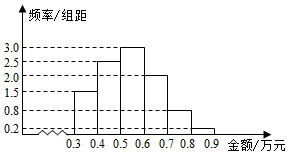 某电子商务公司随机抽取l000名网络购物者进行调查,这1000名购物者2015年网上购物金额(单位:万元)均在区间[0.3,0.9]内,样本分组为:[0.3,0.4),[0.4,0.5),
某电子商务公司随机抽取l000名网络购物者进行调查,这1000名购物者2015年网上购物金额(单位:万元)均在区间[0.3,0.9]内,样本分组为:[0.3,0.4),[0.4,0.5),| 购物金额分组 | [0.3,0.5) | [0.5,0.6) | [0.6,0.8) | [0.8,0.9] |
| 发放金额 | 50 | 100 | 150 | 200 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
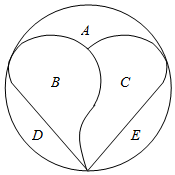 如图所示,积木拼盘由A、B、C、D、E五块积木组成,若每块积木都要涂一种颜色,且为了体现拼盘的特色,相邻的区域需涂不同的颜色(如:A与B为相邻区域,A与D为不相邻区域),现有五种不同的颜色可供挑选,则可组成的不同的积木拼盘的种数是( )
如图所示,积木拼盘由A、B、C、D、E五块积木组成,若每块积木都要涂一种颜色,且为了体现拼盘的特色,相邻的区域需涂不同的颜色(如:A与B为相邻区域,A与D为不相邻区域),现有五种不同的颜色可供挑选,则可组成的不同的积木拼盘的种数是( )| A. | 780 | B. | 840 | C. | 900 | D. | 960 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 1 | C. | 3 | D. | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com