
分析 根据积分的几何意义进行表示即可.
解答 解:(1)y=0,y=$\sqrt{x}$,得到x=0,
S=${∫}_{0}^{2}$$\sqrt{x}$dx=$\frac{2}{3}$${x}^{\frac{3}{2}}$|${\;}_{0}^{2}$=$\frac{2}{3}$$\frac{4\sqrt{2}}{3}$,
(2)由$\left\{\begin{array}{l}{y=x-2}\\{x={y}^{2}}\end{array}\right.$解得y=-1或y=2,
则S=${∫}_{-1}^{2}$(y+2-y2)dy=($\frac{1}{2}{y}^{2}+2y-\frac{1}{3}{y}^{3}$)|${\;}_{-1}^{2}$=(2+4-$\frac{8}{3}$)-($\frac{1}{2}$-2+$\frac{1}{3}$)=$\frac{9}{2}$
点评 本题主要考查积分的几何意义,注意利用积分表示面积时,函数f(x)满足f(x)≥0.


 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
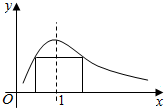 一矩形的一边在x轴上,另两个顶点在函数y=$\frac{2x}{1+{x}^{2}}$(x>0)的图象上,如图,则此矩形绕x轴旋转而成的几何体的体积的最大值是( )
一矩形的一边在x轴上,另两个顶点在函数y=$\frac{2x}{1+{x}^{2}}$(x>0)的图象上,如图,则此矩形绕x轴旋转而成的几何体的体积的最大值是( )| A. | π | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 与m,n都相交 | B. | 与m,n中至少有一条相交 | ||
| C. | 与m,n都不相交 | D. | 与m,n中一条相交 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 零向量平行于任何向量 | |
| B. | 对于平面上意三点A,B,C,一定有$\overrightarrow{AB}$+$\overrightarrow{BC}$=$\overrightarrow{AC}$ | |
| C. | 若$\overrightarrow{AB}$=m$\overrightarrow{CD}$(m∈R),则$\overrightarrow{AB}$∥$\overrightarrow{CD}$ | |
| D. | 若$\overrightarrow{a}$=m$\overrightarrow{i}$,$\overrightarrow{b}$=n$\overrightarrow{j}$,则当m=n时,$\overrightarrow{a}=\overrightarrow{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com