
| A. | $\frac{7}{12}$ | B. | $\frac{5}{12}$ | C. | $\frac{1}{3}+ln2$ | D. | $\frac{1}{6}+ln2$ |
分析 根据题目给出的函数定义,写出分段函数f(x)=min{x2,$\frac{1}{x}$},由图象直观看出所求面积的区域,然后直接运用定积分求解阴影部分的面积.
解答 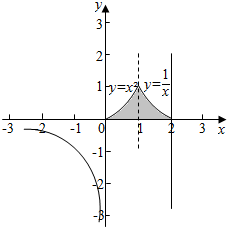 解:由$\frac{1}{x}$=x2,得:x=1,
解:由$\frac{1}{x}$=x2,得:x=1,
又当x<0时,$\frac{1}{x}$<x2,
所以,根据新定义有f(x)=min{x2,$\frac{1}{x}$}=$\left\{\begin{array}{l}{{x}^{2},0<x≤1}\\{\frac{1}{x},x<0或x>1}\end{array}\right.$,
图象如图,
所以,由函数f(x)的图象与x轴、x=2直线所围成的封闭图形为图中阴影部分,
其面积为S=${∫}_{0}^{1}$x2dx+${∫}_{1}^{2}$$\frac{1}{x}$dx=$\frac{1}{3}{x}^{3}$|${\;}_{0}^{1}$+lnx|${\;}_{1}^{2}$=$\frac{1}{3}$+ln2,
故选:C.
点评 本题考查了定积分在求面积中的应用,考查了新定义,训练了学生的作图能力,解答要用数形结合画出所求面积的区域,此题是中档题.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:选择题
| A. | [1,2] | B. | [0,1] | C. | (-1,0) | D. | (0,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
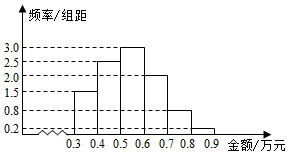 某电子商务公司随机抽取l000名网络购物者进行调查,这1000名购物者2015年网上购物金额(单位:万元)均在区间[0.3,0.9]内,样本分组为:[0.3,0.4),[0.4,0.5),
某电子商务公司随机抽取l000名网络购物者进行调查,这1000名购物者2015年网上购物金额(单位:万元)均在区间[0.3,0.9]内,样本分组为:[0.3,0.4),[0.4,0.5),| 购物金额分组 | [0.3,0.5) | [0.5,0.6) | [0.6,0.8) | [0.8,0.9] |
| 发放金额 | 50 | 100 | 150 | 200 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | l.. | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 1 | C. | 3 | D. | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com