练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知点C为y2=2px（p＞0）的准线与x轴的交点，点F为焦点，点A、B为抛物线上两个点，若
    FA
    +
    FB
    +2
    FC
    =
    0，
    则向量
    FA
    与
    FB
    的夹角为
    2π
    3
    2π
    3
    ．
    分析：设出点A，B的坐标，利用点A、B是抛物线上的两个点，
    FA
    +
    FB
    +2
    FC
    =
    0，
    可求
    FA
    ，
    FB
    的坐标，再利用向量的夹角公式，即可得出结论．
    解答：解：设A（x1，y1），B（x2，y2），抛物线y2=2px（p＞0）的准线与x轴的交点C（-
    p
    2
    ，0），焦点F（
    p
    2
    ，0）
    ∵
    FA
    +
    FB
    +2
    FC
    =
    0

    ∴（x1-
    p
    2
    ，y1）+（x2-
    p
    2
    ，y2）+（-2p，0）=（0，0）
    ∴x1+x2=3p，y1+y2=0
    ∵y12=2px1，y22=2px2，
    ∴y12+y22=2p（x1+x2）
    ∴y12=y22=3p2，x1=x2=
    3
    2
    p
    ∴
    FA
    =（p，
    		3
    p），
    FB
    =（p，-
    		3
    p）
    设向量
    FA
    ，
    FB
    的夹角为α，则cosα=
    FA
    •
    FB
    |
    FA
    |•|
    FB
    |
    =
    p2-3p 2
    4p2
    =-
    1
    2

    ∵α∈[0，π]
    ∴α=
    2π
    3

    故答案为：
    2π
    3
    ．
    点评：本题考查抛物线的简单性质，向量知识的运用，考查向量的夹角公式，解题的关键是确定向量的坐标．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知点M是抛物线y2=2px（p＞0）位于第一象限部分上的一点，且点M与焦点F的距离|MF|=2p，则点M的坐标为（　　）
    A、（
    3p
    2
    ，
    		3
    p）
    B、（
    3p
    2
    ，-
    		3
    p）
    C、（
    3p
    2
    ，±
    		3
    p）
    D、（
    		3
    p，
    3p
    2
    ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （文科做（1）（2）（4），理科全做）
    已知过抛物线C1：y2=2px（p＞0）焦点F的直线交抛物线于A（x1，y1），B（x2，y2）两点 
    （1）证明：y1y2=-p2且（y1+y2）2=2p（x1+x2-p）；
    （2）点Q为线段AB的中点，求点Q的轨迹方程；
    （3）若x1=1，x2=4，以坐标轴为对称轴的椭圆或双曲线C2过A、B两点，求曲线C1和C2的方程；
    （4）在（3）的条件下，若曲线C2的两焦点分别为F1、F2，线段AB上有两点C（x3，y3），D（x4，y4）（x3＜x4），满足：①S△F1F2A-S△F1F2C=S△F1F2D-S△F1F2B，②AB=3CD．在线段F1 F2上是否存在一点P，使PD=
    		11
    ，若存在，求出点P的坐标；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在平面直角坐标系中，O为坐标原点，已知两点M（1，-3）、N（5，1），若点C满足
    OC
    =t
    OM
    +(1-t)
    ON
    (t∈R)    ，点C的轨迹与抛物线：y2=2px（p＞0）交于D、E两点．
    （1）
    OD
    ⊥OE
    ，求抛物线的方程；
    （2）过动点（a，0）且斜率为1的直线l与该抛物线交于不同的两点A、B，且|AB|≤2p．
    （i）求a的取值范围；
    （ii）若线段AB的垂直平分线交x轴于点Q，求△QAB面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源：上海市进才中学2007届高三理科月考六数学试题 题型：044

    已知抛物线C：y2＝2px(p＞0)，直线l交C于E、F两点．

    (1)求证：命题“若直线l过点A(2p，0)，则∠EOF＝90°(O为坐标原点)”是真命题；

    (2)写出(1)中命题的逆命题，判断它是真命题还是假命题，并说明理由；

    (3)将点A(2p，0)向右或向左移动为点A(c，0)，直线l过点A交C于E、F两点．当c＞2p及0＜c＜2p时，分别猜测∠EOF大小的变化情况(只须写出结论，不必证明)．

    查看答案和解析>>

    科目：高中数学 来源：2010-2011学年浙江省宁波市万里国际学校高三（上）期中数学试卷（理科）（解析版） 题型：选择题

    已知点M是抛物线y2=2px（p＞0）位于第一象限部分上的一点，且点M与焦点F的距离|MF|=2p，则点M的坐标为（ ）
    A．（，p）
    B．（，p）
    C．（，p）
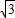    D．（p，）

    查看答案和解析>>

    同步练习册答案