
如图(示意),公路AM、AN围成的是一块顶角为α的角形耕地,其中tanα=-2.在该块土地中P处有一小型建筑,经测量,它到公路AM,AN的距离分别为3km,km.现要过点P修建一条直线公路BC,将三条公路围成的区域ABC建成一个工业园.为尽量减少耕地占用,问如何确定B点的位置,使得该工业园区的面积最小?并求最小面积.

当AB=5km时,该工业园区的面积最小,最小面积为15km2.
【解析】
试题分析:先确定点P的位置,再利用BC的斜率表示工业园区的面积,利用导数求其最值. 以A为原点,AB为x轴,建立平面直角坐标系.因为tanα=-2,故直线AN的方程是y=-2x.设点P(x0,y0).因为点P到AM的距离为3,故y0=3.由P到直线AN的距离为 ,得
,得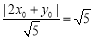 ,解得x0=1或x0=-4(舍去),所以点P(1,3).显然直线BC的斜率存在.设直线BC的方程为y-3=k(x-1),k∈(-2,0).令y=0得xB=1-
,解得x0=1或x0=-4(舍去),所以点P(1,3).显然直线BC的斜率存在.设直线BC的方程为y-3=k(x-1),k∈(-2,0).令y=0得xB=1-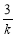 .由
.由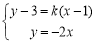 解得yC=
解得yC= .设△ABC的面积为S,则S=
.设△ABC的面积为S,则S=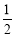 xB?yC=
xB?yC= .由S?=
.由S?=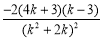 =0得k=-
=0得k=-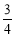 或k=3.所以当k=-
或k=3.所以当k=-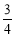 时,即AB=5时,S取极小值,也为最小值15.
时,即AB=5时,S取极小值,也为最小值15.
试题解析:【解析】
如图1,以A为原点,AB为x轴,建立平面直角坐标系.
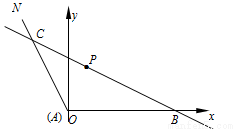
因为tanα=-2,故直线AN的方程是y=-2x.
设点P(x0,y0).
因为点P到AM的距离为3,故y0=3.
由P到直线AN的距离为 ,
,
得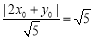 ,解得x0=1或x0=-4(舍去),
,解得x0=1或x0=-4(舍去),
所以点P(1,3). 4分
显然直线BC的斜率存在.设直线BC的方程为y-3=k(x-1),k∈(-2,0).
令y=0得xB=1-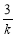 . 6分
. 6分
由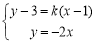 解得yC=
解得yC= . 8分
. 8分
设△ABC的面积为S,则S=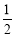 ?xB?yC=
?xB?yC= 10分
10分
由S?=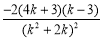 =0得k=-
=0得k=-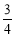 或k=3.
或k=3.
当-2<k<-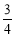 时,S?<0,S单调递减;当-
时,S?<0,S单调递减;当-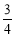 <k<0时,S?>0,S单调递增. 13分
<k<0时,S?>0,S单调递增. 13分
所以当k=-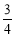 时,即AB=5时,S取极小值,也为最小值15.
时,即AB=5时,S取极小值,也为最小值15.
答:当AB=5km时,该工业园区的面积最小,最小面积为15km2. 16分
考点:利用导数求函数最值


科目:高中数学 来源:2015届江苏省南京市高三9月调研考试文科数学试卷(解析版) 题型:填空题
已知函数f(x)=x-1-(e-1)lnx,其中e为自然对数的底,则满足f(ex)<0的x的取值范围
为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com