
【题目】如图,三棱柱![]() 的底面是正三角形,
的底面是正三角形,![]() 底面
底面![]() ,M为
,M为![]() 的中点.
的中点.
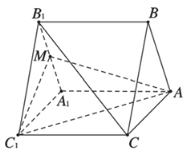
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() ,且沿侧棱
,且沿侧棱![]() 展开三棱柱的侧面,得到的侧面展开图的对角线长为
展开三棱柱的侧面,得到的侧面展开图的对角线长为![]() ,求作点
,求作点![]() 在平面
在平面![]() 内的射影H,请说明作法和理由,并求线段AH的长.
内的射影H,请说明作法和理由,并求线段AH的长.
【答案】(1)证明见解析(2)作法见解析,理由见解析,![]()
【解析】
(1)连结![]() ,交
,交![]() 于点O,连结OM,先证明
于点O,连结OM,先证明![]() ,进而得证;
,进而得证;
(2)过![]() 作
作![]() 于H,通过证明
于H,通过证明![]() 平面
平面![]() ,可得证;在
,可得证;在![]() 中,由射影定理,有
中,由射影定理,有![]() ,可计算得AH.
,可计算得AH.
(1)如图,
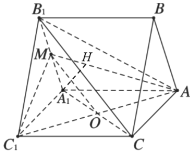
连结![]() ,交
,交![]() 于点O,连结OM.
于点O,连结OM.
因为三棱柱![]() 的侧面
的侧面![]() 是平行四边形,所以O为
是平行四边形,所以O为![]() 中点,
中点,
因为M为![]() 的中点,所以
的中点,所以![]() .
.
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)过![]() 作
作![]() 于H,
于H,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,
因为![]() 是正三角形,M为
是正三角形,M为![]() 的中点,
的中点,
所以![]() ,又
,又![]() ,
,![]()
![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,所以
,所以![]() ,
,
又因为![]() ,
,![]()
![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() 于H,
于H,
所以H为点![]() 在平面
在平面![]() 内的射影.
内的射影.
因为三棱柱侧面展开图是矩形,
且对角线长为![]() ,侧棱
,侧棱![]() ,
,
所以三棱柱底面周长为![]() .
.
又因为三棱柱的底面是正三角形,
所以底面边长![]()
![]() ,
,
在![]() 中,
中,![]()
![]() ,
,
由射影定理,有![]() ,
,
即![]() ,所以
,所以![]() .
.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:高中数学 来源: 题型:
【题目】某校高三1班共有48人,在“六选三”时,该班共有三个课程组合:理化生、理化历、史地政其中,选择理化生的共有24人,选择理化历的共有16人,其余人选择了史地政,现采用分层抽样的方法从中抽出6人,调查他们每天完成作业的时间.
(1)应从这三个组合中分别抽取多少人?
(2)若抽出的6人中有4人每天完成六科(含语数英)作业所需时间在3小时以上,2人在3小时以内.现从这6人中随机抽取3人进行座谈.
用X表示抽取的3人中每天完成作业所需时间在3小时以上的人数,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() .
.
(1)若![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(2)若![]() ,且函数
,且函数![]() 在区间
在区间![]() 内有两个极值点,求实数a的取值范围;
内有两个极值点,求实数a的取值范围;
(3)求证:对任意的正数a,都存在实数t,满足:对任意的![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲居住在城镇的![]() 处,准备开车到单位
处,准备开车到单位![]() 处上班,若该地各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图(例如:
处上班,若该地各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图(例如:![]() 算作两个路段:路段
算作两个路段:路段![]() 发生堵车事件的概率为
发生堵车事件的概率为![]() ,路段
,路段![]() 发生堵车事件的概率为
发生堵车事件的概率为![]() ).
).

(1)请你为甲选择一条由![]() 到
到![]() 的最短路线
的最短路线
(即此人只选择从西向东和从南向北的路线),
使得途中发生堵车事件的概率最小;
(2)设甲在路线![]() 中遇到的堵车次数为随机变量
中遇到的堵车次数为随机变量![]() ,求
,求![]() 的数学期望
的数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为实数.
为实数.
(1)当![]() 时,判断函数
时,判断函数![]() 在其定义域上的单调性;
在其定义域上的单调性;
(2)是否存在实数![]() ,使得对任意的
,使得对任意的![]() ,
,![]() 恒成立?若不存在,请说明理由;若存在,求出
恒成立?若不存在,请说明理由;若存在,求出![]() 的值并加以证明.
的值并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车品牌为了了解客户对于其旗下的五种型号汽车的满意情况,随机抽取了一些客户进行回访,调查结果如下表:
汽车型号 | I | II | III | IV | V |
回访客户(人数) | 250 | 100 | 200 | 700 | 350 |
满意率 | 0.5 | 0.3 | 0.6 | 0.3 | 0.2 |
满意率是指:某种型号汽车的回访客户中,满意人数与总人数的比值.
假设客户是否满意互相独立,且每种型号汽车客户对于此型号汽车满意的概率与表格中该型号汽车的满意率相等.
(1)从所有的回访客户中随机抽取1人,求这个客户满意的概率;
(2)从I型号和V型号汽车的所有客户中各随机抽取1人,设其中满意的人数为![]() ,求
,求![]() 的分布列和期望;
的分布列和期望;
(3)用 “![]() ”, “
”, “![]() ”, “
”, “![]() ”, “
”, “![]() ”, “
”, “![]() ”分别表示I, II, III, IV, V型号汽车让客户满意, “
”分别表示I, II, III, IV, V型号汽车让客户满意, “![]() ”, “
”, “![]() ”, “
”, “![]() ”, “
”, “![]() ”, “
”, “![]() ” 分别表示I, II, III, IV, V型号汽车让客户不满意.写出方差
” 分别表示I, II, III, IV, V型号汽车让客户不满意.写出方差![]() 的大小关系.
的大小关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了解学生的体育锻炼时间,采用简单随机抽样方法抽取了100名学生,对其平均每日参加体育锻炼的时间(单位:分钟)进行调查,按平均每日体育锻炼时间分组统计如下:
分组 |
|
|
|
|
|
|
男生人数 | 2 | 16 | 19 | 18 | 5 | 3 |
女生人数 | 3 | 20 | 10 | 2 | 1 | 1 |
若将平均每日参加体育锻炼的时间不低于120分钟的学生称为“锻炼达人”.
(1)将频率视为概率,估计该校4000名学生中“锻炼达人”有多少?
(2)从这100名学生的“锻炼达人”中按性别分层抽取5人参加某项体育活动.
①求男生和女生各抽取了多少人?
②若从这5人中随机抽取2人作为组长候选人,求抽取的2人中男女各1人的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com