
【题目】某学校为了解学生的体育锻炼时间,采用简单随机抽样方法抽取了100名学生,对其平均每日参加体育锻炼的时间(单位:分钟)进行调查,按平均每日体育锻炼时间分组统计如下:
分组 |
|
|
|
|
|
|
男生人数 | 2 | 16 | 19 | 18 | 5 | 3 |
女生人数 | 3 | 20 | 10 | 2 | 1 | 1 |
若将平均每日参加体育锻炼的时间不低于120分钟的学生称为“锻炼达人”.
(1)将频率视为概率,估计该校4000名学生中“锻炼达人”有多少?
(2)从这100名学生的“锻炼达人”中按性别分层抽取5人参加某项体育活动.
①求男生和女生各抽取了多少人?
②若从这5人中随机抽取2人作为组长候选人,求抽取的2人中男女各1人的概率.
【答案】(1)400;(2)①男生和女生应分别抽取4人和1人;②![]() .
.
【解析】
(1)求出100名学生中的“锻炼达人”人数,可得4000名学生中“锻炼达人”的人数;
(2)①因为100名学生的“锻炼达人”按性别中的男女之比为![]() ,可得男生和女生各抽取的人数;
,可得男生和女生各抽取的人数;
②求出从5人中随机抽取2人的抽取方法数及抽取的2人中恰好男女各1人的抽法,可得抽取的2人中男女各1人的概率.
解:(1)100名学生中的“锻炼达人”人数为![]() ,
,
由此估计,4000名学生中“锻炼达人”有![]() 人,
人,
(2)①因为100名学生的“锻炼达人”按性别中的男女之比为![]() ,
,
故按要求抽取5人,男生和女生应分别抽取4人和1人.
②记这4名男生为a,b,c,d,1名女生记为A,
则从这5人中随机抽取2人,其抽取方法共有10种:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
其中抽取的2人中恰好男女各1人的抽法共有4种:
![]() ,
,![]() ,
,![]() ,
,![]() .
.
故抽取的2人中恰好男女各1人的概率为:
![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 的底面是正三角形,
的底面是正三角形,![]() 底面
底面![]() ,M为
,M为![]() 的中点.
的中点.
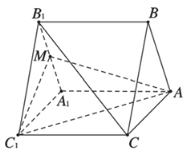
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() ,且沿侧棱
,且沿侧棱![]() 展开三棱柱的侧面,得到的侧面展开图的对角线长为
展开三棱柱的侧面,得到的侧面展开图的对角线长为![]() ,求作点
,求作点![]() 在平面
在平面![]() 内的射影H,请说明作法和理由,并求线段AH的长.
内的射影H,请说明作法和理由,并求线段AH的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.![]() 为曲线
为曲线![]() 上的动点,点
上的动点,点![]() 在射线
在射线![]() 上,且满足
上,且满足![]() .
.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设![]() 与
与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 且倾斜角为
且倾斜角为![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某中学高三文科班学生的数学与语文的水平测试成绩抽样统计如下表:
数学(x)
语文(y) | 90分~100分 (数A) | 80分~90分 (数B) | 60分~80分 (数C) |
90分~100分 (语A) | 20 | 7 | 5 |
80分~90分 (语B) | 18 | 9 | 6 |
60分~80分 (语C) | 4 | a | b |
设x,y分别表示数学成绩与语文成绩,若抽取学生n人,成绩在90分~100分者记为A等级(优秀),成绩在80分~90分者记为B等级(良好),成绩在60分~80分者记为C等级(及格).例如:表中数学成绩为A等级的共有![]() 人.已知x与y均为B等级的概率是0.09.
人.已知x与y均为B等级的概率是0.09.
(1)若在该样本中,数学成绩良好率是30%,求a,b的值;
(2)在语文成绩为C等级的学生中,已知![]() ,
,![]() ,求数学成绩为B等级的人数比C等级的人数少的概率.
,求数学成绩为B等级的人数比C等级的人数少的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且以椭圆
,且以椭圆![]() 的两焦点和短轴的一个端点为顶点的三角形的周长恰为
的两焦点和短轴的一个端点为顶点的三角形的周长恰为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)动直线![]() 与抛椭圆
与抛椭圆![]() 相交于
相交于![]() ,
,![]() 两点,问:在
两点,问:在![]() 轴上是否存在定点
轴上是否存在定点![]() (其中
(其中![]() ,使得向量
,使得向量![]() 与向量
与向量![]() 共线(其中
共线(其中![]() 为坐标原点)?若存在,求出点
为坐标原点)?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将420名工人编号为:001,002,![]() ,420,采用系统抽样的方法抽取一个容量为60的样本,且随机抽得的号码为005.这420名工人来自三个工厂,从001到200为
,420,采用系统抽样的方法抽取一个容量为60的样本,且随机抽得的号码为005.这420名工人来自三个工厂,从001到200为![]() 工厂,从201到355为
工厂,从201到355为![]() 工厂,从356到420为
工厂,从356到420为![]() 工厂,则三个工厂被抽中的工人数依次为( )
工厂,则三个工厂被抽中的工人数依次为( )
A.28,23,9B.27,23,10C.27,22,11D.28,22,10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现在给出三个条件:①a=2;②B![]() ;③c
;③c![]() b.试从中选出两个条件,补充在下面的问题中,使其能够确定△ABC,并以此为依据,求△ABC的面积.
b.试从中选出两个条件,补充在下面的问题中,使其能够确定△ABC,并以此为依据,求△ABC的面积.
在△ABC中,a、b、c分别是角A、B、C的对边,且满足![]() ,求△ABC的面积(选出一种可行的方案解答,若选出多个方案分别解答,则按第一个解答记分)
,求△ABC的面积(选出一种可行的方案解答,若选出多个方案分别解答,则按第一个解答记分)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为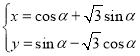 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,取相同长度单位建立极坐标系,直线
轴的正半轴为极轴,取相同长度单位建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 和直线
和直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)直线![]() 与
与![]() 轴交点为
轴交点为![]() ,经过点
,经过点![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() ,
,![]() 两点,证明:
两点,证明:![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com