
【题目】在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.![]() 为曲线
为曲线![]() 上的动点,点
上的动点,点![]() 在射线
在射线![]() 上,且满足
上,且满足![]() .
.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设![]() 与
与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 且倾斜角为
且倾斜角为![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】设有下列四个命题:
![]() :若
:若![]() ,则
,则![]() ;
;
![]() :若
:若![]() ,则
,则![]() ;
;
![]() :“
:“![]() ”是“
”是“![]() 为奇函数”的充要条件;
为奇函数”的充要条件;
![]() :“等比数列
:“等比数列![]() 中,
中,![]() ”是“等比数列
”是“等比数列![]() 是递减数列”的充要条件.
是递减数列”的充要条件.
其中,真命题的是![]()
![]()
A. ![]() ,
,![]() B.
B. ![]() ,
,![]() C.
C. ![]() ,
,![]() D.
D. ![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆M经过点F(1,0),且与直线l:x=﹣1相切,动圆圆心M的轨迹记为曲线C
(1)求曲线C的轨迹方程
(2)若点P在y轴左侧(不含y轴)一点,曲线C上存在不同的两点A、B,满足PA,PB的中点都在曲线C上,设AB中点为E,证明:PE垂直于y轴.
查看答案和解析>>
科目:高中数学 来源: 题型:
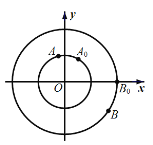
【题目】如图,点![]() 分别是圆心在原点,半径为
分别是圆心在原点,半径为![]() 和
和![]() 的圆上的动点.动点
的圆上的动点.动点![]() 从初始位置
从初始位置![]() 开始,按逆时针方向以角速度
开始,按逆时针方向以角速度![]() 作圆周运动,同时点
作圆周运动,同时点![]() 从初始位置
从初始位置![]() 开始,按顺时针方向以角速度
开始,按顺时针方向以角速度![]() 作圆周运动.记
作圆周运动.记![]() 时刻,点
时刻,点![]() 的纵坐标分别为
的纵坐标分别为![]() .
.
(Ⅰ)求![]() 时刻,
时刻,![]() 两点间的距离;
两点间的距离;
(Ⅱ)求![]() 关于时间
关于时间![]() 的函数关系式,并求当
的函数关系式,并求当![]() 时,这个函数的值域.
时,这个函数的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线y2=2px(p>0)的焦点为F,点A(2,y0)为抛物线上一点,且|AF|=4.
(1)求抛物线的方程;
(2)直线l:y=x+m与抛物线交于不同两点P,Q,若![]() ,其中O为坐标原点,求m的值.
,其中O为坐标原点,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2018·湖南师大附中摸底)已知直线l经过点P(-4,-3),且被圆(x+1)2+(y+2)2=25截得的弦长为8,则直线l的方程是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,点P是圆C:
,点P是圆C:![]() 上的任意一点,线段PQ的垂直平分线与直线CP交于点M.
上的任意一点,线段PQ的垂直平分线与直线CP交于点M.
![]() 求点M的轨迹方程;
求点M的轨迹方程;
![]() 过点
过点![]() 作直线与点M的轨迹交于点E,过点
作直线与点M的轨迹交于点E,过点![]() 作直线与点M的轨迹交于点
作直线与点M的轨迹交于点![]() F不重合
F不重合![]() ,且直线AE和直线BF的斜率互为相反数,直线EF的斜率是否为定值,若为定值,求出直线EF的斜率;若不是定值,请说明理由.
,且直线AE和直线BF的斜率互为相反数,直线EF的斜率是否为定值,若为定值,求出直线EF的斜率;若不是定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某乡镇政府为了解决农村教师的住房问题,计划征用一块土地盖一幢建筑总面积为10000![]() 公寓楼(每层的建筑面积相同).已知士地的征用费为
公寓楼(每层的建筑面积相同).已知士地的征用费为![]() ,土地的征用面积为第一层的
,土地的征用面积为第一层的![]() 倍,经工程技术人员核算,第一层建筑费用为
倍,经工程技术人员核算,第一层建筑费用为![]() ,以后每增高一层,其建筑费用就增加
,以后每增高一层,其建筑费用就增加![]() ,设这幢公寓楼高层数为n,总费用为
,设这幢公寓楼高层数为n,总费用为![]() 万元.(总费用为建筑费用和征地费用之和)
万元.(总费用为建筑费用和征地费用之和)
(1)若总费用不超过835万元,求这幢公寓楼最高有多少层数?
(2)试设计这幢公寓的楼层数,使总费用最少,并求出最少费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com