
【题目】函数![]()
![]() 部分图象如图所示.
部分图象如图所示.
(1)求![]() 的最小正周期及解析式;
的最小正周期及解析式;
(2)设![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,最小值为
,最小值为![]() .
.
【解析】
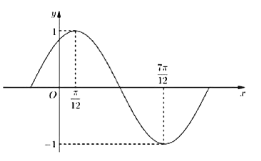
(1)由图可知A=1,![]() ,从而可求ω;再由图象经过点(
,从而可求ω;再由图象经过点(![]() ,1),可求得
,1),可求得![]() ;
;
(2)依题意g(x)化简整理为g(x)=![]() sin(2x
sin(2x![]() ),再利用正弦函数的性质结合x的范围求得g(x)的最大值和最小值.
),再利用正弦函数的性质结合x的范围求得g(x)的最大值和最小值.
(1)由图可知:![]() ,A=1,
,A=1,
∴T=π,
∴ω![]() 2,
2,
∴f(x)=cos(2x+![]() )
)
又∵图象经过点![]() ,
,
∴1=cos(2![]() ),
),
∴![]() 2kπ,k∈Z,
2kπ,k∈Z,
∴![]() 2kπ,k∈Z,
2kπ,k∈Z,
又∵|![]() |
|![]() ,
,
∴![]() ,
,
∴解析式为f(x)=cos(2x![]() );
);
(2)g(x)=f(x)+sin2x
=cos(2x![]() )+sin2x
)+sin2x
=cos2xcos![]() sin2xsin
sin2xsin![]()
![]() sin2x
sin2x![]() cos2x
cos2x
=![]() sin(2x
sin(2x![]() );当
);当![]() 时,2x
时,2x![]() ,
,
当2x![]() 时,即x=
时,即x=![]() 时,g(x)的最大值为
时,g(x)的最大值为![]() ,当2x
,当2x![]() ,即x=
,即x=![]() 时g(x)的最小值为
时g(x)的最小值为![]() ,
,
综上所述,![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,最小值为
,最小值为![]() .
.


 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:高中数学 来源: 题型:
【题目】为了分析某个高三学生的学习状态.现对他前5次考试的数学成绩x,物理成绩y进行分析.下面是该生前5次考试的成绩.
数学 | 120 | 118 | 116 | 122 | 124 |
物理 | 79 | 79 | 77 | 82 | 83 |
附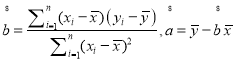 .
.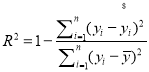 .
.
![]() 已知该生的物理成绩y与数学成绩x是线性相关的,求物理成绩y与数学成绩x的回归直线方程;
已知该生的物理成绩y与数学成绩x是线性相关的,求物理成绩y与数学成绩x的回归直线方程;
![]() 我们常用
我们常用![]() 来刻画回归的效果,其中
来刻画回归的效果,其中![]() 越接近于1,表示回归效果越好.求
越接近于1,表示回归效果越好.求![]() .
.
![]() 已知第6次考试该生的数学成绩达到132,请你估计第6次考试他的物理成绩大约是多少?
已知第6次考试该生的数学成绩达到132,请你估计第6次考试他的物理成绩大约是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F为椭圆C:![]() 的左焦点,过F作两条互相垂直的直线
的左焦点,过F作两条互相垂直的直线![]() ,
,![]() ,直线
,直线![]() 与C交于A,B两点,直线
与C交于A,B两点,直线![]() 与C交于D,E两点,则四边形ADBE的面积最小值为( )
与C交于D,E两点,则四边形ADBE的面积最小值为( )
A.4B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,
,![]() ,在椭圆L上的点
,在椭圆L上的点![]() 满足
满足![]() ,且
,且![]() ,
,![]() ,
,![]() 成等差数列.
成等差数列.
(1)求椭圆L的方程;
(2)过点A作两条倾斜角互补的直线![]() ,
,![]() ,它们与椭圆L的另一个交点分别为B,C,试问直线BC的斜率是否是定值?若是,求出该斜率;若不是,请说明理由.
,它们与椭圆L的另一个交点分别为B,C,试问直线BC的斜率是否是定值?若是,求出该斜率;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.![]() 为曲线
为曲线![]() 上的动点,点
上的动点,点![]() 在射线
在射线![]() 上,且满足
上,且满足![]() .
.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设![]() 与
与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 且倾斜角为
且倾斜角为![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系中,坐标原点为![]() ,点
,点![]() ,
,![]() 、
、![]() 两点分别在
两点分别在![]() 轴和
轴和![]() 轴上运动,并且满足
轴上运动,并且满足![]() ,
,![]() ,动点
,动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求动点![]() 的轨迹方程;
的轨迹方程;
(2)作曲线![]() 的任意一条切线(不含
的任意一条切线(不含![]() 轴)
轴)![]() ,直线
,直线![]() 与切线
与切线![]() 相交于
相交于![]() 点,直线
点,直线![]() 与切线
与切线![]() 、
、![]() 轴分别相交于
轴分别相交于![]() 点与
点与![]() 点,试探究
点,试探究![]() 的值是否为定值,若为定值请求出该定值;若不为定值请说明理由.
的值是否为定值,若为定值请求出该定值;若不为定值请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com