
【题目】正方体ABCD﹣A1B1C1D1中,BB1与平面ACD1所成角的正弦值为( )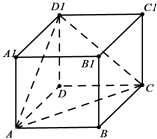
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:连接B1D,BD,则:AC⊥BD,
又AC⊥BB1 , ∴AC⊥平面BB1D,∴B1D⊥AC,
同理B1D⊥AD1 , ∴B1D⊥平面ACD1;
设B1D交平面ACD1于E,连接EA,EC,ED1 , B1D1 , B1A,B1C,
则容易证明△B1ED1 , △B1EC,△B1EA,三个三角形全等,
取CD1中点F,连接EF,则EF⊥CD1 , ![]() ,
,
设正方体的棱长为a,则 ![]() ,
, ![]() ,
, 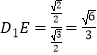 ;
;
通过前面知∠DD1E是DD1和平面ACD1所成的角,
又BB1∥DD1 ,
∴它也是BB1与平面ACD1所成角,则:
cos∠DD1E= ![]() ,
,
∴sin∠DD1E= ![]() .
.
故选B.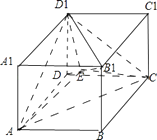
【考点精析】解答此题的关键在于理解空间角的异面直线所成的角的相关知识,掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则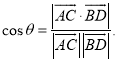 .
.


科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点P是圆O:x2+y2=1与x轴正半轴的交点,半径OA在x轴的上方,现将半径OA绕原点O逆时针旋转 ![]() 得到半径OB.设∠POA=x(0<x<π),
得到半径OB.设∠POA=x(0<x<π), ![]() .
. 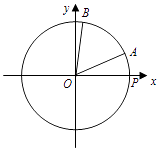
(1)若 ![]() ,求点B的坐标;
,求点B的坐标;
(2)求函数f(x)的最小值,并求此时x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生态公园的平面图呈长方形(如图),已知生态公园的长AB=8(km),宽AD=4(km),M,N分别为长方形ABCD边AD,DC的中点,P,Q为长方形ABCD边AB,BC(不含端点)上的一点.现公园管理处拟修建观光车道P﹣Q﹣N﹣M﹣P,要求观光车道围成四边形(如图阴影部分)的面积为15(km2),设BP=x(km),BQ=y(km), 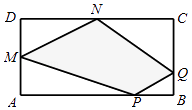
(1)试写出y关于x的函数关系式,并求出x的取值范围;
(2)若B为公园入口,P,Q为观光车站,观光车站P位于线段AB靠近入口B的一侧.经测算,每天由B入口至观光车站P,Q乘坐观光车的游客数量相等,均为1万人,问如何确定观光车站P,Q的位置,使所有游客步行距离之和最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场在一部向下运行的手扶电梯终点的正上方竖直悬挂一幅广告画.如图,该电梯的高AB为4米,它所占水平地面的长AC为8米.该广告画最高点E到地面的距离为10.5米.最低点D到地面的距离6.5米.假设某人的眼睛到脚底的距离MN为1.5米,他竖直站在此电梯上观看DE的视角为θ. 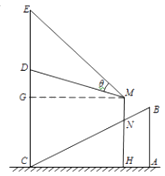
(1)设此人到直线EC的距离为x米,试用x表示点M到地面的距离;
(2)此人到直线EC的距离为多少米,视角θ最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+(a﹣2)x﹣2,a∈R.
(1)若关于x的不等式f(x)≤0的解集为[﹣1,2],求实数a的值;
(2)当a<0时,解关于x的不等式f(x)≤0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在△ABC中,角A,B,C的对边分别是a,b,c,且bsinA+acosB=0.
(1)求角B的大小;
(2)若b=2,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的最下正周期为π,且点P(
)的最下正周期为π,且点P( ![]() ,2)是该函数图象的一个人最高点.
,2)是该函数图象的一个人最高点.
(1)求函数f(x)的解析式;
(2)若x∈[﹣ ![]() ,0],求函数y=f(x)的值域;
,0],求函数y=f(x)的值域;
(3)把函数y=f(x)的图线向右平移θ(0<θ< ![]() )个单位,得到函数y=g(x)在[0,
)个单位,得到函数y=g(x)在[0, ![]() ]上是单调增函数,求θ的取值范围.
]上是单调增函数,求θ的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com