
设函数
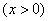 .
.
(1)求函数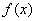 的最小值;
的最小值;
(2)设
 ,讨论函数
,讨论函数 的单调性;
的单调性;
(3)斜率为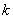 的直线与
的直线与 交于
交于 ,
,
 两点,求证:
两点,求证: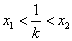 .
.
(1)解:f'(x)=lnx+1(x>0),令f'(x)=0,得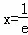 .
.
∵当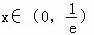 时,f'(x)<0;当
时,f'(x)<0;当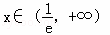 时,
时,
f'(x)>0,
∴当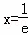 时,
时,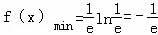 .----------------- 4分
.----------------- 4分
(2)F(x)=ax2+lnx+1(x>0), .
.
①当a≥0时,恒有F'(x)>0,F(x)在(0,+∞)上是增函数;
②当a<0时,
令F'(x)>0,得2ax2+1>0,解得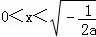 ;
;
令F'(x)<0,得2ax2+1<0,解得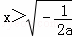 .
.
综上,当a≥0时,F(x)在(0,+∞)上是增函数;
当a<0时,F(x)在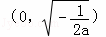 上单调递增,在
上单调递增,在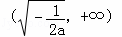 上单调递减.------------------------------------8分
上单调递减.------------------------------------8分
(3)证: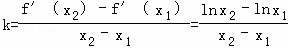 .
.
要证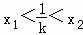 ,即证
,即证 ,等价于证
,等价于证 ,令
,令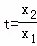 ,
,
则只要证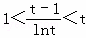 ,由t>1知lnt>0,
,由t>1知lnt>0,
故等价于证lnt<t﹣1<tlnt(t>1)(*).
①设g(t)=t﹣1﹣lnt(t≥1),则 ,
,
故g(t)在[1,+∞)上是增函数,
∴当t>1时,g(t)=t﹣1﹣lnt>g(1)=0,即t﹣1>lnt(t>1).
②设h(t)=tlnt﹣(t﹣1)(t≥1),则h'(t)=lnt≥0(t≥1),故h(t)在[1,+∞)上是增函数,
∴当t>1时,h(t)=tlnt﹣(t﹣1)>h(1)=0,即t﹣1<tlnt(t>1).
由①②知(*)成立,得证.


科目:高中数学 来源: 题型:
为了了解小学五年级学生的体能情况,抽取了实验小学五年级部分学生
进行踢毽子测试,将所得的数据整理后画出频率分布直方图(如图),已知图中从左到右的
前三个小组的频率分别是0.1,0.3,0.4,第一小组的频数是5.
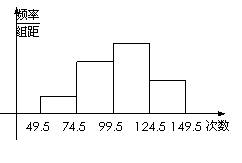 (Ⅰ)求第四小组的频率和参加这次测试的学生人数;
(Ⅰ)求第四小组的频率和参加这次测试的学生人数;
(Ⅱ)在这次测试中,问学生踢毽子次数的中位数落
在第几小组内?
(Ⅲ)在这次跳绳测试中,规定跳绳次数在110以上
的为优秀,试估计该校此年级跳绳成绩的优秀率
是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
某商场对顾客实行购物优惠活动,规定一次购物付款总额:
(1)如果不超过200元,则不给予优惠;
(2)如果超过200元但不超过500元,则按标价给予9折优惠;
(3)如果超过500元,其500元内的按第(2)条给予优惠,超过500元的部分给予7折优惠.
某人两次去购物,分别付款168元和423元,假设他一次性购买上述两次同样的商品,则应付款是
A .413.7元 B. 513.7元
C. 546.6元 D .548.7元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com