练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．已知$\frac{1-sinα}{\sqrt{3}cos（\frac{π}{2}-α）}$=tan10°，则锐角α=50°．

    分析 解方程得出sinα=$\frac{1}{\sqrt{3}tan10°+1}$，利用三角变换化简求解即可．

    解答 解：∵$\frac{1-sinα}{\sqrt{3}cos（\frac{π}{2}-α）}$=tan10°，
    ∴1-sinα=$\sqrt{3}tan10°$sina，
    即sinα=$\frac{1}{\sqrt{3}tan10°+1}$=$\frac{cos1′0°}{\sqrt{3}sin10°+cos10°}$=$\frac{sos10°}{2sin（10°+30°）}$=$\frac{cos10°}{2sin40°}$=$\frac{sin80°}{2sin40°}$=cos40°=sin50°
    ∴锐角α=50°．
    故答案为：50°．

    点评 本题利用方程考查了三角函数的变换求值，关键是灵活运用两角和差公式，诱导公式求解，注意角之间的联系．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    19．已知$\overrightarrow{a}$=（1，2sinθ），$\overrightarrow{b}$=（cosθ，-2），且$\overrightarrow{a}$$⊥\overrightarrow{b}$．
    （1）求tanθ的值；
    （2）求$\frac{1}{sin2θ+co{s}^{2}θ}$的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．已知函数f（x）=（x+2）（x2+ax-5）的图象关于点（-2，0）中心对称，设关于x的不等式f（x+m）＜f（x）的解集为A，若（-5，-2）⊆A，则实数m的取值范围是{3，-3}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

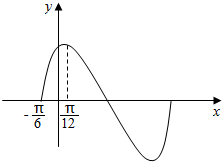    18．如图是函数f（x）=2sinωx•cosωx+2$\sqrt{3}$cos2ωx-$\sqrt{3}$（ω＞0）的一部分图象．
    （1）求ω的值；
    （2）在△ABC中，已知a=3，b+c=6，求f（A-$\frac{π}{3}$）的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．设函数f（x）=x2+ax+b，若方程f（x）=x（b∈Z）在（1，3）上存在两个不等的实根，求b的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．判断函数f（x）=$\left\{\begin{array}{l}{x（1-x）（x≥0）}\\{x（1+x）（x＜0）}\end{array}\right.$的奇偶性．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知直线l：y=mx+m（|m|＜1．m≠0），抛物线C：y2=4x
    （1）求证：l与抛物线C必相交于两点
    （2）求截得的弦AB的长
    （3）当m为何值时，弦AB的中点在直线x-y-3=0上．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．求证：f（x）=$\frac{-1}{x}$在（-∞，0）上递增，在（0，+∞）上递增．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．数列$\frac{1}{2}$，$\frac{3}{4}$，$\frac{5}{8}$，$\frac{7}{16}$的一个通项公式是an=$\frac{2n-1}{{2}^{n}}$．

    查看答案和解析>>

    同步练习册答案