解:(Ⅰ)因为f'(x)=-3x
2-4mx-m
2,所以f'(2)=-12-8m-m
2=-5,
解得:m=-1或m=-7,又m>-2,所以m=-1,
由f'(x)=-3x
2+4x-1=0,解得x
1=1,
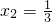
,
列表如下:
| x | 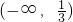 |  |  | 1 | (1,+∞) |
| f'(x) | - | 0 | + | 0 | - |
| f(x) | ↘ | 极小值 | ↗ | 极大值2 | ↘ |
所以
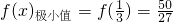
,f(x)
极大值=f(1)=2,
因为f(x)=-x
3+2x
2-x+2=-(x-2)(x
2+1),
所以函数f(x)的零点是x=2.
(Ⅱ)由(Ⅰ)知,当x∈[0,1]时,
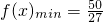
,
“对任意x
1∈[0,1],存在x
2∈(0,1],使f(x
1)>g(x
2)”等价于“f(x)在[0,1]上的最小值大于g(x)在(0,1]上的最小值,
即当x∈(0,1]时,
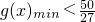
”,
因为
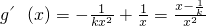
,
①当k<0时,因为x∈(0,1],
所以
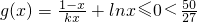
,符合题意;
②当0<k≤1时,

,
所以x∈(0,1]时,g'(x)≤0,g(x)单调递减,
所以
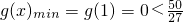
,符合题意;
③当k>1时,

,
所以
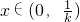
时,g'(x)<0,g(x)单调递减,
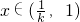
时,g'(x)>0,g(x)单调递增,
所以x∈(0,1]时,
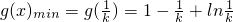
,
令

(0<x<1),则
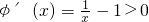
,
所以φ(x)在(0,1)上单调递增,
所以x∈(0,1)时,

,即

,
所以
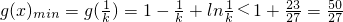
,符合题意,
综上所述,若对任意x
1∈[0,1],存在x
2∈(0,1],使f(x
1)>g(x
2)成立,
则实数k的取值范围是(-∞,0)∪(0,+∞).
分析:(Ⅰ)由f(x)在x=2处的切线与直线x-5y-12=0垂直可得f′(2)=-5,从而可求得m值,利用导数即可求得其极值,对于f(x)的零点可转化为f(x)=0的根求解;
(Ⅱ)“对任意x
1∈[0,1],存在x
2∈(0,1],使f(x
1)>g(x
2)”等价于“f(x)在[0,1]上的最小值大于g(x)在(0,1]上的最小值,
由(Ⅰ)易求f(x)
min,利用导数可求g(x)在(0,1]上的最小值,注意按k的范围进行讨论.
点评:本题考查导数的综合应用:求函数极值、最值及不等式恒成立问题,考查分类讨论思想,考查学生综合运用知识分析问题解决问题的能力.

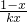 +lnx,若对任意x1∈[0,1],存在x2∈(0,1],使f(x1)>g(x2)成立,求实数k的取值范围.
+lnx,若对任意x1∈[0,1],存在x2∈(0,1],使f(x1)>g(x2)成立,求实数k的取值范围.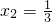 ,
,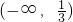



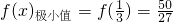 ,f(x)极大值=f(1)=2,
,f(x)极大值=f(1)=2,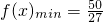 ,
,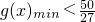 ”,
”,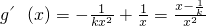 ,
,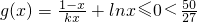 ,符合题意;
,符合题意; ,
,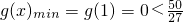 ,符合题意;
,符合题意; ,
,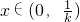 时,g'(x)<0,g(x)单调递减,
时,g'(x)<0,g(x)单调递减,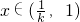 时,g'(x)>0,g(x)单调递增,
时,g'(x)>0,g(x)单调递增,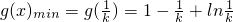 ,
, (0<x<1),则
(0<x<1),则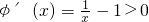 ,
, ,即
,即 ,
,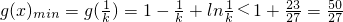 ,符合题意,
,符合题意,

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案