
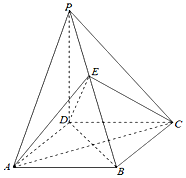
 (文科)底面ABCD是菱形,∠BAD=60°,AB=2,PD=$\sqrt{6}$,O为AC与BD的交点,E为棱PB上一点.
(文科)底面ABCD是菱形,∠BAD=60°,AB=2,PD=$\sqrt{6}$,O为AC与BD的交点,E为棱PB上一点.分析 (Ⅰ)证明AC⊥PD,AC⊥BD,推出AC⊥平面PBD.然后证明平面EAC⊥平面PBD.
(Ⅱ)取AD中点H,连结BH,说明BD⊥平面PAD,然后利用等体积法求解几何体的体积即可.
解答 (文科)试题解析:
(Ⅰ)证明:∵PD⊥平面ABCD,AC?平面ABCD,
∴AC⊥PD.∵四边形ABCD是菱形,∴AC⊥BD,
又∵PD∩BD=D,AC⊥平面PBD.
而AC?平面EAC,∴平面EAC⊥平面PBD.
(Ⅱ)解:∵PD∥平面EAC,平面EAC∩平面PBD=OE,∴PD∥OE,
∵O是BD中点,∴E是PB中点.
取AD中点H,连结BH,∵四边形ABCD是菱形,∠BAD=60°,
∴BH⊥AD,又BH⊥PD,AD∩PD=D,∴BD⊥平面PAD,BH=$\frac{\sqrt{3}}{2}$AB=$\sqrt{3}$.
∴${V}_{P-EAD}={V}_{E-PAD}=\frac{1}{2}{V}_{B-PAD}$=$\frac{1}{2}$×$\frac{1}{3}$×S△PAD×BH=$\frac{1}{6}×\frac{1}{2}×2×\sqrt{6}×\sqrt{3}$=$\frac{\sqrt{2}}{2}$.
点评 本题考查直线与平面垂直的判定定理以及平面与平面垂直的判定定理的应用,几何体的体积的求法,考查空间想象能力以及计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
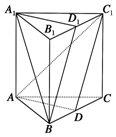 如图所示,已知三棱柱ABC-A1B1C1中,D是BC的中点,D1是B1C1的中点,设平面A1D1B∩平面ABC=l1,平面ADC1∩平面A1B1C1=l2,
如图所示,已知三棱柱ABC-A1B1C1中,D是BC的中点,D1是B1C1的中点,设平面A1D1B∩平面ABC=l1,平面ADC1∩平面A1B1C1=l2,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{3}{2}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了了解中学生的身高情况,对某中学同龄的若干女生身高进行测量,将所得数据整理后,画出频率分布直方图如图所示,已知图中从左到右五个小组的频率分别为0.017,0.050,0.100,0.133,0.300,第三小组的频数为6.
为了了解中学生的身高情况,对某中学同龄的若干女生身高进行测量,将所得数据整理后,画出频率分布直方图如图所示,已知图中从左到右五个小组的频率分别为0.017,0.050,0.100,0.133,0.300,第三小组的频数为6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com