
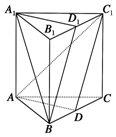
 如图所示,已知三棱柱ABC-A1B1C1中,D是BC的中点,D1是B1C1的中点,设平面A1D1B∩平面ABC=l1,平面ADC1∩平面A1B1C1=l2,
如图所示,已知三棱柱ABC-A1B1C1中,D是BC的中点,D1是B1C1的中点,设平面A1D1B∩平面ABC=l1,平面ADC1∩平面A1B1C1=l2,分析 连接DD1.过B点作直线l1'∥AD,证明l1'即为l1,可得l1∥AD∥A1D1;过C1作直线l2'∥A1D1,证明l2'即为l2,l2∥AD∥A1D1;即可得证l1∥l2.
解答 (1)证明: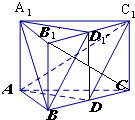 连接DD1.在四边形BDD1B1中,BD=$\frac{1}{2}$BC=$\frac{1}{2}$B1C1=B1D1,BD∥B1D1,
连接DD1.在四边形BDD1B1中,BD=$\frac{1}{2}$BC=$\frac{1}{2}$B1C1=B1D1,BD∥B1D1,
所以四边形BDD1B1为平行四边形,
所以DD1=BB1=AA1①,且DD1∥BB1∥AA1②;由①、②得:
四边形ADD1A1为平行四边形,
所以AD∥A1D1③;
过B点作直线l1'∥AD,由③知l1'∥A1D1,由于AD在面ABC中,
A1D1在面A1B1C1中,
所以l1'∥面ABC,l1'∥A1B1C1,由于B点同时在面ABC和面A1B1C1中,
所以l1'同时在面ABC和面A1B1C1中,即l1'为面ABC和面A1B1C1的交线,
所以l1'即为l1,
所以l1∥AD∥A1D1④;
过C1作直线l2'∥A1D1,同上可以证明l2'即为l2,l2∥AD∥A1D1⑤;
由④、⑤即得l1∥l2.
(2)解:分别取AA1,A1C1,AB的中点E,F,G,连EF,EG,FG
则∠GEF为所求角或其补角,令棱长为2,则GE=EF=$\sqrt{2}$,GF=$\sqrt{5}$,
由余弦定理得cos∠GEF=-$\frac{1}{4}$,故A1B与AC1所成角的余弦值为$\frac{1}{4}$.
点评 本题在三棱柱中证明面面平行,并且求A1B与AC1所成角的余弦值.着重考查了线面平行、面面平行的判定定理等知识,属于中档题.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(1,\frac{3}{2})$ | B. | $(\frac{{\sqrt{3}}}{2},\frac{3}{2})$ | C. | $(\frac{1}{2},\frac{3}{2})$ | D. | $(\frac{1}{2},\frac{3}{2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 7 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
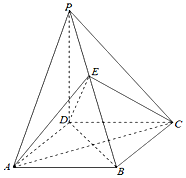 (文科)底面ABCD是菱形,∠BAD=60°,AB=2,PD=$\sqrt{6}$,O为AC与BD的交点,E为棱PB上一点.
(文科)底面ABCD是菱形,∠BAD=60°,AB=2,PD=$\sqrt{6}$,O为AC与BD的交点,E为棱PB上一点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com