
���� ��1����F1��-c��0����F2��c��0����A��0��1����B��0��-1����ֱ��AF1����Ϊ��x-cy+c=0��������֪$\frac{2c}{\sqrt{1+{c}^{2}}}$=$\sqrt{2}$���ɴ��������Բ���̣�
��2����AB��y=k��x-2�������뷽�̵ã�1+2k2��x2-8k2x+8k2-2=0���ɴ����ø����б�ʽ��Τ�ﶨ������Բ���ʣ������ʵ��t��ȡֵ��Χ��
��� �⣺��1����F1��F2�ֱ�����Բ$\frac{x^2}{a^2}$+y2=1��a��1�������ҽ��㣬A��B�ֱ�Ϊ��Բ���ϡ��¶��㣬
����F1��-c��0����F2��c��0����A��0��1����B��0��-1��
��ֱ��AF1����Ϊ��x-cy+c=0��
��F2��ֱ��AF1�ľ���Ϊ$\sqrt{2}$��
��������֪$\frac{2c}{\sqrt{1+{c}^{2}}}$=$\sqrt{2}$�����c=1��
��a=$\sqrt{2}$������Բ����Ϊ$\frac{x^2}{2}+{y^2}=1$��
��2��������ֱ֪��AB��б�ʴ��ڣ�
��AB��y=k��x-2����A��x1��y1����B��x2��y2����P��x��y��
���뷽����Ԫ�ɵã�1+2k2��x2-8k2x+8k2-2=0��
��$��=64{k^4}-4��2{k^2}+1����8{k^2}-2����0����{k^2}��\frac{1}{2}$��
��$\overrightarrow{OA}+\overrightarrow{OB}=t\overrightarrow{OP}$����$x=\frac{{{x_1}+{x_2}}}{t}=\frac{{8{k^2}}}{{k��1+2{k^2}��}}��y=\frac{-4k}{{t��1+2{k^2}��}}$��
�ߵ�P����Բ�ϣ���$\frac{{{{��8{k^2}��}^2}}}{{{k^2}{{��1+2{k^2}��}^2}}}+2\frac{{{{��-4k��}^2}}}{{{t^2}{{��1+2{k^2}��}^2}}}=2$��
��16k2=t2��1+2k2������${t}^{2}=8-\frac{8}{1+2{k}^{2}}$��
��${k}^{2}��\frac{1}{2}$����t2�ʣ�0��4����
��t�ʣ�-2��0���ȣ�0��2����
��ʵ��t��ȡֵ��Χ�ǣ�-2��0���ȣ�0��2����
���� ���⿼����Բ���̵�������ʵ����ȡֵ��Χ�������е��⣬ע������б�ʽ��Τ�ﶨ������Բ���ʵĺ������ã�


 �ľ�ͼ���ʱ�ȷ�ϵ�д�
�ľ�ͼ���ʱ�ȷ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �ȱ������� | B�� | ֱ�������� | C�� | ���������� | D�� | ����ֱ�������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {x|2��x��3} | B�� | {x|3��x��4} | C�� | {x|2��x��4} | D�� | {x|2��x��4} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 15 | B�� | 37 | C�� | 27 | D�� | 64 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | f��x��=1��g��x��=x0 | B�� | f��x��=|x|��g��x��=$\left\{\begin{array}{l}x��x��0\\-x��x��0\end{array}\right.$ | ||
| C�� | f��x��=x+2��g��x��=$\frac{{{x^2}-4}}{x-2}$ | D�� | f��x��=x��g��x��=��$\sqrt{x}$��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
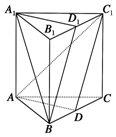 ��ͼ��ʾ����֪������ABC-A1B1C1�У�D��BC���е㣬D1��B1C1���е㣬��ƽ��A1D1B��ƽ��ABC=l1��ƽ��ADC1��ƽ��A1B1C1=l2��
��ͼ��ʾ����֪������ABC-A1B1C1�У�D��BC���е㣬D1��B1C1���е㣬��ƽ��A1D1B��ƽ��ABC=l1��ƽ��ADC1��ƽ��A1B1C1=l2���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com