练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

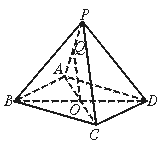
     P是平行四边形ABCD外的一点，Q是PA的中点，求证：PC∥平面BDQ．


    证明：如图，连结AC交BD于O

    ∵　ABCD是平行四边形，∴　AO＝OC

    连结OQ，则OQ平面BDQ，

    且OQ是△APC的中位线

    ∴　PC∥OQ，又PC在平面BDQ外∴　PC∥平面BDQ．

     



    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014-2015学年浙江省杭州地区七校高二下学期期中联考文科数学试卷（解析版） 题型：选择题

    有下列四个命题：

    ①“平面内一个动点到两个定点的距离之和为定长，则动点的轨迹为椭圆”；

    ②“若q≤1，则方程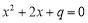有实根”的否命题；

    ③“若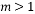，则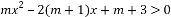的解集为R”的逆命题.

    ④“若两条直线没有公共点，则这两条直线是异面直线”的逆否命题.

    其中真命题的序号有（ ）

    A.②③ B.①③④ C.①③ D.①④

    查看答案和解析>>

    科目：高中数学 来源：2014-2015学年福建省高一下学期第一次月考数学试卷（解析版） 题型：选择题

    阅读如下程序框图，如果输出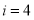，那么空白的判断框中应填人的条件是 （ ）

    A．S<8? B．S<12? C．S<14? D．S<16?

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    下列说法正确的是（    ）

    A．空间中不同三点确定一个平面      B．空间中两两相交的三条直线确定一个平面   

    C．梯形确定一个平面                D．一条直线和一个点确定一个平面

    查看答案和解析>>

    科目：高中数学 来源： 题型：


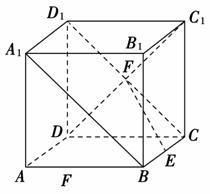
    正方体ABCD－A1B1C1D1中，E、F分别是线段BC、C1D的中点，则直线A1B与直线EF的位置关系是(　　)

    A．相交              B．平行

    C．异面              D．以上都有可能

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图， 四棱柱的底面是正方形， 为底面中心， 平面，．

    （1） 证明: 平面//平面；

    （2） 求三棱柱的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


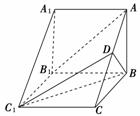
    如图，在三棱柱ABC－A1B1C1中，侧棱AA1⊥底面ABC，AB⊥BC，D为AC的中点，AA1＝AB＝2.

    (1)求证：AB1∥平面BC1D；

    (2)若BC＝3，求三棱锥D－BC1C的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     如图，已知正三棱柱ABCA1B1C1的底面边长为2厘米，高为5厘米，一质点自点A出发，沿着三棱柱的侧面绕行两周到达点A1的最短路线的长为多少厘米？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在正方体ABCD－A1B1C1D1中，P为DD1中点，O为底面ABCD中心，

    求证：B1O⊥平面PAC

    查看答案和解析>>

    同步练习册答案