若函数f(x)=x3-3x+a有三个不同的零点,求实数a的取值范围.
(本小题满分12分)
解:由函数f(x)=x
3-3x+a有三个不同的零点,
则函数f(x)有两个极值点,极小值小于0,极大值大于0;
由f′(x)=3x
2-3=3(x+1)(x-1)=0,解得x
1=1,x
2=-1,
所以函数f(x)的两个极,x∈(-∞,-1),f′(x)>0,x∈(-1,1),f′(x)<0,x∈(1,+∞),f′(x)>0,
∴函数的极小值f(1)=a-2和极大值f(-1)=a+2.
因为函数f(x)=x
3-3x+a有三个不同的零点,
所以
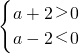
,解之,得-2<a<2.
故实数a的取值范围是(-2,2).
分析:已知条件转化为函数有两个极值点,并且极小值小于0,极大值大于0,求解即可.
点评:本题是中档题,考查函数的导数与函数的极值的关系,考查转化思想,计算能力.

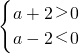 ,解之,得-2<a<2.
,解之,得-2<a<2.
