
已知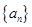 是递增的等差数列,
是递增的等差数列, ,
,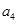 是方程
是方程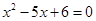 的根。
的根。
(I)求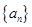 的通项公式;
的通项公式;
(II)求数列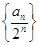 的前
的前 项和.
项和.
(1) ;(2)
;(2)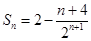 .
.
解析试题分析:(1)根据题中所给一元二次方程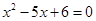 ,可运用因式分解的方法求出它的两根为2,3,即可得出等差数列中的
,可运用因式分解的方法求出它的两根为2,3,即可得出等差数列中的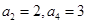 ,运用等差数列的定义求出公差为d,则
,运用等差数列的定义求出公差为d,则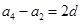 ,故
,故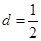 ,从而
,从而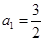 .即可求出通项公式;(2)由第(1)小题中已求出通项,易求出:
.即可求出通项公式;(2)由第(1)小题中已求出通项,易求出: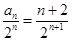 ,写出它的前n项的形式:
,写出它的前n项的形式: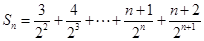 ,观察此式特征,发现它是一个差比数列,故可采用错位相减的方法进行数列求和,即两边同乘
,观察此式特征,发现它是一个差比数列,故可采用错位相减的方法进行数列求和,即两边同乘 ,即:
,即: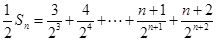 ,将两式相减可得:
,将两式相减可得: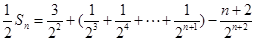
 ,所以
,所以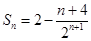 .
.
试题解析:(1)方程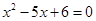 的两根为2,3,由题意得
的两根为2,3,由题意得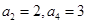 .
.
设数列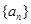 的公差为d,则
的公差为d,则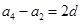 ,故
,故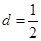 ,从而
,从而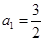 .
.
所以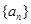 的通项公式为
的通项公式为 .
.
(2)设 的前n项和为
的前n项和为 ,由(1)知
,由(1)知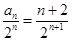 ,则
,则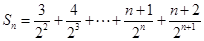 ,
,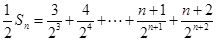 .
.
两式相减得

所以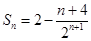 .
.
考点:1.一元二次方程的解法;2.等差数列的基本量计算;3.数列的求和


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:高中数学 来源: 题型:解答题
设等差数列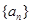 的公差为
的公差为 ,点
,点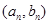 在函数
在函数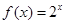 的图象上(
的图象上( ).
).
(1)若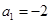 ,点
,点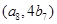 在函数
在函数 的图象上,求数列
的图象上,求数列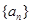 的前
的前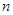 项和
项和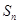 ;
;
(2)若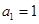 ,学科网函数
,学科网函数 的图象在点
的图象在点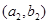 处的切线在
处的切线在 轴上的截距为
轴上的截距为 ,求数列
,求数列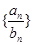 的前
的前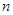 项和
项和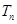 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com