【题目】某校团委对“学生性别与中学生追星是否有关”作了一次调查，利用
列联表，由计算得
,参照下表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
得到正确结论是( )
A. 有99%以上的把握认为“学生性别与中学生追星无关”
B. 有99%以上的把握认为“学生性别与中学生追星有关”
C. 在犯错误的概率不超过0.5%的前提下，认为“学生性别与中学生追星无关”
D. 在犯错误的概率不超过0.5%的前提下，认为“学生性别与中学生追星有关”
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案科目：高中数学 来源： 题型：
【题目】为了政府对过热的房地产市场进行调控决策，统计部门对城市人和农村人进行了买房的心理预期调研，用简单随机抽样的方法抽取110人进行统计，得到如下列联表：
买房 | 不买房 | 纠结 | |
城市人 | 5 | 15 | |
农村人 | 20 | 10 |
已知样本中城市人数与农村人数之比是3：8．
分别求样本中城市人中的不买房人数和农村人中的纠结人数；
用独立性检验的思想方法说明在这三种买房的心理预期中哪一种与城乡有关？
参考公式：
．
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】甲、乙两同学在复习数列时发现原来曾经做过的一道数列问题因纸张被破坏，导致一个条件看不清，具体如下：等比数列
的前n项和为
，已知_____，
（1）判断
，
，
的关系；
（2）若
，设
，记
的前n项和为
，证明：
.
甲同学记得缺少的条件是首项a1的值，乙同学记得缺少的条件是公比q的值，并且他俩都记得第（1）问的答案是，，成等差数列.如果甲、乙两同学记得的答案是正确的，请你通过推理把条件补充完整并解答此题.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，直线
的参数方程为
（
为参数）.以坐标原点为极点，
轴的非负半轴为极轴且取相同的单位长度建立极坐标系，圆
的极坐标方程为
.
（1）求直线的普通方程与圆的直角坐标方程；
（2）设动点
在圆上，动线段
的中点
的轨迹为
，与直线交点为
，且直角坐标系中，
点的横坐标大于
点的横坐标，求点的直角坐标.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
.
（1）求证：当x∈(0,π]时，f(x)<1；
（2）求证：当m＞2时，对任意x0∈(0,π] ，存在x1∈(0,π]和x2∈(0,π](x1≠x2)使g(x1)=g(x2)=f(x0)成立.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在三棱锥
中，平面
平面
，
和
均是等腰直角三角形，
，
，
、
分别为
、
的中点.
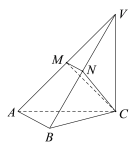
（Ⅰ）求证：
平面
；
（Ⅱ）求证：
；
（Ⅲ）求直线与平面所成角的正弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆C：
1（a
b0）的左、右焦点分别为F1，F2，点P为椭圆C上不与左右顶点重合的动点，设I，G分别为△PF1F2的内心和重心.当直线IG的倾斜角不随着点P的运动而变化时，椭圆C的离心率为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
