
【题目】如图,在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() 和
和![]() 均是等腰直角三角形,
均是等腰直角三角形,![]() ,
,![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点.
的中点.
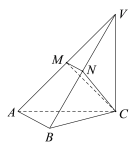
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求证:![]() ;
;
(Ⅲ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(Ⅰ)证明见解析;(Ⅱ)证明见解析;(Ⅲ)![]() .
.
【解析】
(Ⅰ)由中位线的性质得出![]() ,然后利用直线与平面平行的判定定理可证明出
,然后利用直线与平面平行的判定定理可证明出![]() 平面
平面![]() ;
;
(Ⅱ)由已知条件可知![]() ,然后利用面面垂直的性质定理可证明出
,然后利用面面垂直的性质定理可证明出![]() 平面
平面![]() ,即可得出
,即可得出![]() ;
;
(Ⅲ)以![]() 为原点,
为原点,![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴建立空间直角坐标系,利用空间向量法求出直线
轴建立空间直角坐标系,利用空间向量法求出直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(Ⅰ)在![]() 中,
中,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,所以
的中点,所以![]() 为中位线,所以
为中位线,所以![]() .
.
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ;
;
(Ⅱ)在等腰直角三角形![]() 中,
中,![]() ,所以
,所以![]() .
.
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]() ,所以
,所以![]() ;
;
(Ⅲ)在平面![]() 内过点
内过点![]() 作
作![]() 垂直于
垂直于![]() ,由(Ⅱ)知,
,由(Ⅱ)知,![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
如图,以![]() 为原点建立空间直角坐标系
为原点建立空间直角坐标系![]() .
.
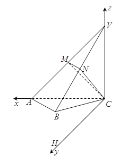
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则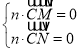 ,即
,即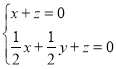 .
.
令![]() 则
则![]() ,
,![]() ,所以
,所以![]() .
.
直线![]() 与平面
与平面![]() 所成角大小为
所成角大小为![]() ,
,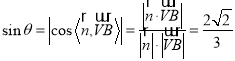 .
.
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在三棱锥A﹣BCD中,点E在BD上,EA=EB=EC=ED,BD![]() CD,△ACD为正三角形,点M,N分别在AE,CD上运动(不含端点),且AM=CN,则当四面体C﹣EMN的体积取得最大值
CD,△ACD为正三角形,点M,N分别在AE,CD上运动(不含端点),且AM=CN,则当四面体C﹣EMN的体积取得最大值![]() 时,三棱锥A﹣BCD的外接球的表面积为_____.
时,三棱锥A﹣BCD的外接球的表面积为_____.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为椭圆
的焦点为椭圆![]() 的右焦点,C的准线与E交于P,Q两点,且
的右焦点,C的准线与E交于P,Q两点,且![]() .
.
(1)求E的方程;
(2)过E的左顶点A作直线l交E于另一点B,且BO(O为坐标原点)的延长线交E于点M,若直线AM的斜率为1,求l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校团委对“学生性别与中学生追星是否有关”作了一次调查,利用![]() 列联表,由计算得
列联表,由计算得![]() ,参照下表:
,参照下表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
得到正确结论是( )
A. 有99%以上的把握认为“学生性别与中学生追星无关”
B. 有99%以上的把握认为“学生性别与中学生追星有关”
C. 在犯错误的概率不超过0.5%的前提下,认为“学生性别与中学生追星无关”
D. 在犯错误的概率不超过0.5%的前提下,认为“学生性别与中学生追星有关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 是椭圆
是椭圆![]() 的左右焦点,椭圆与
的左右焦点,椭圆与![]() 轴正半轴交于点
轴正半轴交于点![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,且
,且![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)![]() 为椭圆
为椭圆![]() 上任意一点,过
上任意一点,过![]() ,
,![]() 分别作直线
分别作直线![]() ,
,![]() ,且
,且![]() 与
与![]() 相交于
相交于![]() 轴上方一点
轴上方一点![]() ,当
,当![]() 时,求
时,求![]() ,
,![]() 两点间距离的最大值.
两点间距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代劳动人民在筑城、筑堤、挖沟、挖渠、建仓、建囤等工程中,积累了丰富的经验,总结出了一套有关体积、容积计算的方法,这些方法以实际问题的形式被收入我国古代数学名著《九章算术》中.《九章算术》将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,如图所示的阳马三视图,则它的体积为( )
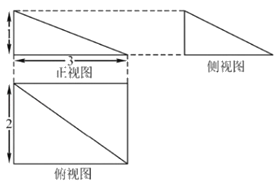
A.![]() B.1C.2D.3
B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex(x+1)2,令f1(x)=f'(x),fn+1(x)=fn'(x),若fn(x)=ex(anx2+bnx+cn),记数列{![]() }的前n项和为Sn,则下列选项中与S2019的值最接近的是( )
}的前n项和为Sn,则下列选项中与S2019的值最接近的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面四边形![]() 中,E,F是
中,E,F是![]() ,
,![]() 中点,
中点,![]() ,
,![]() ,
,![]() ,将
,将![]() 沿对角线
沿对角线![]() 折起至
折起至![]() ,使平面
,使平面![]() 平面
平面![]() ,则四面体
,则四面体![]() 中,下列结论不正确的是( )
中,下列结论不正确的是( )
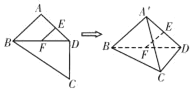
A.![]() 平面
平面![]() B.异面直线
B.异面直线![]() 与
与![]() 所成的角为90°
所成的角为90°
C.异面直线![]() 与
与![]() 所成的角为60°D.直线
所成的角为60°D.直线![]() 与平面
与平面![]() 所成的角为30°
所成的角为30°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com