
【题目】已知抛物线![]() 的焦点为椭圆
的焦点为椭圆![]() 的右焦点,C的准线与E交于P,Q两点,且
的右焦点,C的准线与E交于P,Q两点,且![]() .
.
(1)求E的方程;
(2)过E的左顶点A作直线l交E于另一点B,且BO(O为坐标原点)的延长线交E于点M,若直线AM的斜率为1,求l的方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据题意,先得到椭圆焦点坐标,再由![]() ,得到
,得到![]() ,根据焦点坐标得到
,根据焦点坐标得到![]() ,两式联立,求出
,两式联立,求出![]() ,
,![]() ,即可得出结果;
,即可得出结果;
(2)先由题意,设直线![]() 的方程为
的方程为![]() ,
,![]() ,联立直线与椭圆方程,求出点
,联立直线与椭圆方程,求出点![]() 坐标,根据对称性,得到
坐标,根据对称性,得到![]() 的坐标,再由直线斜率公式,即可求出结果.
的坐标,再由直线斜率公式,即可求出结果.
(1)因为抛物线![]() 的焦点为
的焦点为![]() ,
,
由题意,可得:椭圆![]() 的两焦点为
的两焦点为![]() ,
,
又抛物线![]() 的准线与
的准线与![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,将
,将![]() 代入椭圆方程得
代入椭圆方程得![]() ,所以
,所以![]() ,则
,则![]() ,即
,即![]() ①,
①,
又![]() ②,根据①②解得:
②,根据①②解得:![]() ,
,![]() ,
,
因此椭圆![]() 的方程为
的方程为![]() ;
;
(2)由(1)得![]() 的左顶点为
的左顶点为![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,
由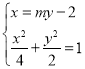 得
得![]() ,所以
,所以![]() ,
,
因此![]() ,所以
,所以![]() ,
,
则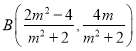 ,
,
又因为![]() (
(![]() 为坐标原点)的延长线交
为坐标原点)的延长线交![]() 于点
于点![]() ,
,
则![]() 与
与![]() 关于原点对称,所以
关于原点对称,所以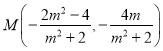 ,
,
因为直线![]() 的斜率为1,
的斜率为1,
所以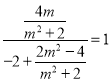 ,解得:
,解得:![]() ,
,
因此,直线![]() 的方程为:
的方程为:![]() .
.


科目:高中数学 来源: 题型:
【题目】已知正方体![]() 的棱长为1,P是空间中任意一点,下列正确命题的个数是( )
的棱长为1,P是空间中任意一点,下列正确命题的个数是( )
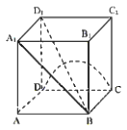
①若P为棱![]() 中点,则异面直线AP与CD所成角的正切值为
中点,则异面直线AP与CD所成角的正切值为![]() ;
;
②若P在线段![]() 上运动,则
上运动,则![]() 的最小值为
的最小值为![]() ;
;
③若P在半圆弧CD上运动,当三棱锥![]() 的体积最大时,三棱锥
的体积最大时,三棱锥![]() 外接球的表面积为
外接球的表面积为![]() ;
;
④若过点P的平面![]() 与正方体每条棱所成角相等,则
与正方体每条棱所成角相等,则![]() 截此正方体所得截面面积的最大值为
截此正方体所得截面面积的最大值为![]()
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,![]() 分别在
分别在![]() 轴,
轴,![]() 轴上运动,
轴上运动,![]() ,点
,点![]() 在线段
在线段![]() 上,且
上,且![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() ,若直线
,若直线![]() ,
,![]() 的斜率之和为2,直线
的斜率之和为2,直线![]() 是否恒过定点?若是,求出定点的坐标;若不是,请说明理由.
是否恒过定点?若是,求出定点的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两同学在复习数列时发现原来曾经做过的一道数列问题因纸张被破坏,导致一个条件看不清,具体如下:等比数列![]() 的前n项和为
的前n项和为![]() ,已知_____,
,已知_____,
(1)判断![]() ,
,![]() ,
,![]() 的关系;
的关系;
(2)若![]() ,设
,设![]() ,记
,记![]() 的前n项和为
的前n项和为![]() ,证明:
,证明:![]() .
.
甲同学记得缺少的条件是首项a1的值,乙同学记得缺少的条件是公比q的值,并且他俩都记得第(1)问的答案是![]() ,
,![]() ,
,![]() 成等差数列.如果甲、乙两同学记得的答案是正确的,请你通过推理把条件补充完整并解答此题.
成等差数列.如果甲、乙两同学记得的答案是正确的,请你通过推理把条件补充完整并解答此题.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设O为坐标原点,动点M在椭圆C![]() 上,过M作x轴的垂线,垂足为N,点P满足
上,过M作x轴的垂线,垂足为N,点P满足![]() .
.
(1)求点P的轨迹方程;
(2)设点![]() 在直线
在直线![]() 上,且
上,且![]() .证明:过点P且垂直于OQ的直线
.证明:过点P且垂直于OQ的直线![]() 过C的左焦点F.
过C的左焦点F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,圆
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与圆
的普通方程与圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设动点![]() 在圆
在圆![]() 上,动线段
上,动线段![]() 的中点
的中点![]() 的轨迹为
的轨迹为![]() ,
,![]() 与直线
与直线![]() 交点为
交点为![]() ,且直角坐标系中,
,且直角坐标系中,![]() 点的横坐标大于
点的横坐标大于![]() 点的横坐标,求点
点的横坐标,求点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() 和
和![]() 均是等腰直角三角形,
均是等腰直角三角形,![]() ,
,![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点.
的中点.
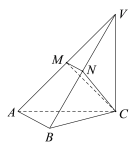
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求证:![]() ;
;
(Ⅲ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(1)求函数![]() 的单调增区间;
的单调增区间;
(2)令![]() ,且函数
,且函数![]() 有三个彼此不相等的零点0,m,n,其中
有三个彼此不相等的零点0,m,n,其中![]() .
.
①若![]() ,求函数
,求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
②若对![]() ,
,![]() 恒成立,求实数t的去取值范围.
恒成立,求实数t的去取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com