
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| y | 40 | 37 | 33 | 30 | 27 | 24 | 20 | 23 | 26 | 31 | 34 | 36 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 2t |
| 3π |
| 2 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| 5π |
| 6 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
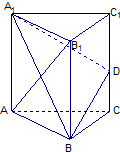 如图,已知三棱柱ABC-A1B1C1的所有棱长都相等,且侧棱垂直于底面,由B沿棱柱侧面经过棱CC1到点A1的最短路线长为2
如图,已知三棱柱ABC-A1B1C1的所有棱长都相等,且侧棱垂直于底面,由B沿棱柱侧面经过棱CC1到点A1的最短路线长为2| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| AB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 产品A(件) | 产品B(件) | ||
| 研制成本与搭载费用之和(万元/件) | 20 | 30 | 计划最大资金额300万元 |
| 样品重量(千克/件) | 10 | 5 | 最大搭载重量110千克 |
| 预计收益(万元/件) | 80 | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| |DP| |
| |MN| |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com