
分析 根据题意,画出图形,结合图形,利用验证的方法求出该不等式x-1<log5(x+3)的所有整数解.
解答 解:∵不等式x-1<log5(x+3),
∴设函数y=x-1,和函数y=log5(x+3),x>3;
在同一坐标系中画出两个函数的图象,如图所示;
则满足不等式的解集应是函数y=x-1在函数y=log5(x+3)图象下方的x的取值;
当x=-2时,y1=-3,y2=log51=0,满足题意;
x=-1时,y1=-2,y2=log52>0,满足题意;
x=0时,y1=-1,y2=log53>0,满足题意;
x=1时,y1=0,y2=log54>0,满足题意;
x=2时,y1=1,y2=log55=1,不满足题意;
综上,不等式的整数解即x的取值是{-2,-1,0,1}.
点评 本题考查了利用对数函数的图象与性质解不等式的应用问题,也考查了数形结合的应用问题,是基础题目.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,+∞) | B. | [-1,0)∪(3,+∞) | C. | (-∞,-1]∪(1,+∞) | D. | (-∞,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
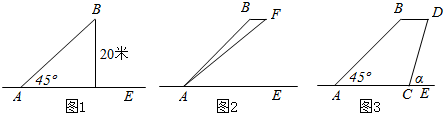
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com