【题目】已知正数
满足
，则
的最大值为（）
A. 
B. 
C. 
D. 
【答案】A
【解析】
令a＝x﹣y，b＝x+y，（x＞y＞0），由此a2+b2＝ab+1可化为（x﹣y）2+（x+y）2＝（x﹣y）（x+y）+1，即x2+3y2＝1（x＞y），然后再令x＝cosα，
，结合三角函数的性质可求.
令a＝x﹣y，b＝x+y，（x＞y＞0），
则a2+b2＝ab+1化为（x﹣y）2+（x+y）2＝（x﹣y）（x+y）+1，即x2+3y2＝1（x＞y），
令x＝cosα，，
∵x＞y＞0，
∴cos
0，
∴0
，
则z＝（
）a+2b＝（
1）（x﹣y）+2（x+y）＝（
1）x﹣（3）y，
＝（1）cosα﹣（3）
＝2
sin（
），
∵0，
∴
，
当sin（）＝1时有最大值2，
故选：A．
黄冈天天练口算题卡系列答案科目：高中数学 来源： 题型：
【题目】为了研究高中学生对乡村音乐的态度（喜欢和不喜欢两种态度）与性别的关系，运用2×2列联表进行独立性检验，经计算K2=8.01，附表如下：
P（K2≥k0） | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
参照附表，得到的正确的结论是（ ）
A. 有99%以上的把握认为“喜欢乡村音乐与性别有关”
B. 有99%以上的把握认为“喜欢乡村音乐与性别无关”
C. 在犯错误的概率不超过0.1%的前提下，认为“喜欢乡村音乐与性别有关”
D. 在犯错误的概率不超过0.1%的前提下，认为“喜欢乡村音乐与性别无关”
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知曲线
的参数方程为
（
为参数），
，
为曲线上的一动点.
（I）求动点对应的参数从
变动到
时，线段
所扫过的图形面积；
（Ⅱ）若直线与曲线的另一个交点为
，是否存在点，使得为线段
的中点？若存在，求出点坐标；若不存在，说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】[选修4-4：坐标系与参数方程]
在直角坐标系
中，曲线
的参数方程为
（
为参数），直线
的方程为
．
（1）以坐标原点为极点，
轴的正半轴为极轴建立极坐标系，求曲线的极坐标方程和直线的极坐标方程；
（2）在（1）的条件下，直线
的极坐标方程为
，设曲线与直线的交于点
和点
，曲线与直线的交于点和点
，求
的面积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】进入
月份，香港大学自主招生开始报名，“五校联盟”统一对五校高三学生进行综合素质测试，在所有参加测试的学生中随机抽取了部分学生的成绩，得到如图所示的成绩频率分布直方图：
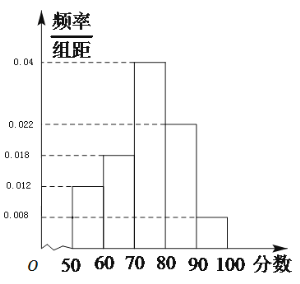
（1）估计五校学生综合素质成绩的平均值；
（2）某校决定从本校综合素质成绩排名前
名同学中，推荐
人参加自主招生考试，若已知名同学中有
名理科生，2名文科生，试求这3人中含文科生的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】若直线
与曲线
满足下列两个条件：①直线在点
处与曲线相切；②曲线在点
附近位于直线的两侧，则称直线在点处“切过”曲线.则下列结论正确的是（ ）
A.直线
在点
处“切过”曲线
B.直线
在点
处“切过”曲线
C.直线
在点处“切过”曲线
D.直线在点处“切过”曲线
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的左、右焦点为
，点
在椭圆
上.
（1）设点
到直线
的距离为
，证明：
为定值；
（2）若
是椭圆上的两个动点（都不与重合），直线
的斜率互为相反数，求直线
的斜率（结果用
表示）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某市为调研学校师生的环境保护意识，决定在本市所有学校中随机抽取60所进行环境综合考评成绩达到80分以上（含80分）为达标．60所学校的考评结果频率分布直方图如图所示（其分组区间为[50，60），[60，70），[70，80），[80，90），[90，100]）．
（Ⅰ）试根据样本估汁全市学校环境综合考评的达标率；
（Ⅱ）若考评成绩在[90.100]内为优秀．且甲乙两所学校考评结果均为优秀从考评结果为优秀的学校中随机地抽取两所学校作经验交流报告，求甲乙两所学校至少有一所被选中的概率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
