练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知以下三视图中有三个同时表示某一个三棱锥，则不是该三棱锥的三视图是 （ ）

    A. B.

    C. D.

    【答案】D

    【解析】试题分析：四个三视图均表示一个高为3，底面为两直角边分别为1，2的棱锥，A与C中俯视图正好旋转，故应是从相反方向进行观察，而其正视图和侧视图中三角形斜边倾斜方向相反，满足实际情况，故A，C表示同一棱锥，设A中观察的正方向为标准正方向，以C表示从后面观察该棱锥，B与D中俯视图正好旋转，故应是从相反方向进行观察，但侧视图中三角形斜边倾斜方向相同，不满足实际情况，故B，D中有一个不与其它三个一样表示同一个棱锥，根据B中正视图与A中侧视图相同，侧视图与C中正视图相同，可判断B是从左边观察该棱锥，故选D

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

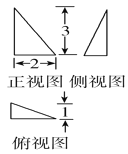
    科目：高中数学 来源： 题型：

    【题目】一鲜花店一个月（30天）某种鲜花的日销售量与销售天数统计如下：

    日销售量（枝）

    0～49

    50～99

    100～149

    150～199

    200～250

    销售天数（天）

    3天

    3天

    15天

    6天

    3天

    将日销售量落入各组区间的频率视为概率．

    （1）试求这30天中日销售量低于100枝的概率；

    （2）若此花店在日销售量低于100枝的6天中选择2天作促销活动，求这2天的日销售量都低于50枝的概率（不需要枚举基本事件）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-5：不等式选讲

    已知函数.

    （1）求不等式的解集；

    （2）设，求的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如今我们的互联网生活日益丰富，除了可以很方便地网购，网上叫外卖也开始成为不少人日常生活中不可或缺的一部分，为了解网络外卖在市的普及情况， 市某调查机构借助网络进行了关于网络外卖的问卷调查，并从参与调查的网民中抽取了200人进行抽样分析，得到表格（单位：人）.

    （1）根据表中数据，能否在犯错误的概率不超过0.15的前提下认为市使用网络外卖的情况与性别有关？

    （2）①现从所抽取的女网民中利用分层抽样的方法再抽取5人，再从这5人中随机选出了3人赠送外卖优惠券，求选出的3人中至少有2人经常使用网络外卖的概率；

    ②将频率视为概率，从市所有参与调查的网民中随机抽取10人赠送礼品，记其中经常使用网络外卖的人数为，求的数学期望和方差.

    参考公式： ，其中.

    参考数据：

    0.15

    0.10

    0.05

    0.025

    0.010

    2.072

    2.706

    3.841

    5.024

    6.635

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】求下列不等式的解集：

    （1）

    （2）

    （3）

    （4）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某个体户计划经销A，B两种商品，据调查统计，当投资额为x(x≥0)万元时，在经销A，B商品中所获得的收益分别为f(x)万元与g(x)万元，其中f(x)＝a(x－1)＋2，g(x)＝6ln(x＋b)(a＞0，b＞0)．已知投资额为零时收益为零．

    (1)求a，b的值；

    (2)如果该个体户准备投入5万元经销这两种商品，请你帮他制定一个资金投入方案，使他能获得最大利润．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

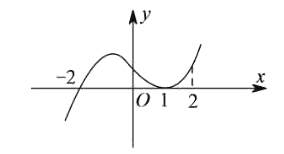
    【题目】如图是函数的导函数的图象，给出下列命题：①-2是函数的极值点；②1是函数的极值点；③在处切线的斜率小于零；④在区间上单调递增.则正确命题的序号是_______.（写出所有正确命题的序号）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分12分）

    已知O为坐标原点，向量，点P满足．

    （Ⅰ）记函数·，求函数的最小正周期；

    （Ⅱ）若O，P，C三点共线，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知

    (1)求函数的极值；

    (2)设，对于任意，总有成立，求实数的取值范围.

    查看答案和解析>>

    同步练习册答案