
分析 以C为坐标原点,CB,CA所在直线为x,y轴建立直角坐标系,表示出点C、B、A,设出点M的坐标,求出$\overrightarrow{MC}$•$\overrightarrow{CB}$的取值范围.
解答 解:如图所示,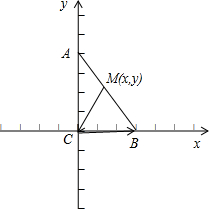
以C为坐标原点,CB,CA所在直线为x,y轴建立直角坐标系,
则C(0,0),B(3,0),A(0,a),其中a>0;
设M(x,y),其中0≤x≤3,
则$\overrightarrow{MC}$=(-x,-y),$\overrightarrow{CB}$=(3,0),
∴$\overrightarrow{MC}$•$\overrightarrow{CB}$=-3x;
由于0≤x≤3,
∴-9≤-3x≤0,
∴$\overrightarrow{MC}$•$\overrightarrow{CB}$的取值范围是[-9,0].
故答案为:[-9,0].
点评 本题考查了平面向量数量积的坐标表示以及应用问题,也考查了函数的最值问题,是基础题目.


科目:高中数学 来源: 题型:解答题
 如图所示,四棱锥S-ABCD的底面四边形ABCD为平行四边形,其中AC⊥BD,且AC、BD相交于O,∠SBC=∠SBA.
如图所示,四棱锥S-ABCD的底面四边形ABCD为平行四边形,其中AC⊥BD,且AC、BD相交于O,∠SBC=∠SBA.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3f(4)<4f(3) | B. | 3f(4)>4f(3) | C. | 3f(3)<4f(2) | D. | 3f(3)>4f(2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
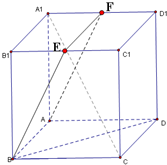 在单位正方体ABCD-A1B1C1D1中,E,F分别是B1C1,A1D1的中点.
在单位正方体ABCD-A1B1C1D1中,E,F分别是B1C1,A1D1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com