Question

6．设方程${log_4}x-{（\frac{1}{4}）^x}=0$、${log_{\frac{1}{4}}}x-{（\frac{1}{4}）^x}=0$的根分别为 x₁、x₂，则（　　）

• A． $\frac{1}{2}$＜x₁x₂＜1
• B． x₁x₂=1
• C． 1＜x₁x₂＜2
• D． x₁x₂≥2

Answer 1

分析 由题意可得，函数y=log₄x和函数y=（$\frac{1}{4}$）^x交点的横坐标为x₁，函数y=${log}_{\frac{1}{4}}$x和函数y=（$\frac{1}{4}$）^x的交点的横坐标为x₂，结合图象可得x₁=$\frac{1}{2}$，1＜x₂＜2，从而得到$\frac{1}{2}$＜x₁x₂＜1，由此求得答案．

解答 解：∵方程log₄x-（$\frac{1}{4}$）^x=0、${log_{\frac{1}{4}}}x-{（\frac{1}{4}）^x}=0$的根分别为x₁、x₂，
∴log₄x=（$\frac{1}{4}$）^x，且${log}_{\frac{1}{4}}$=（$\frac{1}{4}$）^x，
故函数y=log₄x和函数y=（$\frac{1}{4}$）^x交点的横坐标为x₁，函数y=${log}_{\frac{1}{4}}$x和函数y=（$\frac{1}{4}$）^x的交点的横坐标为x₂，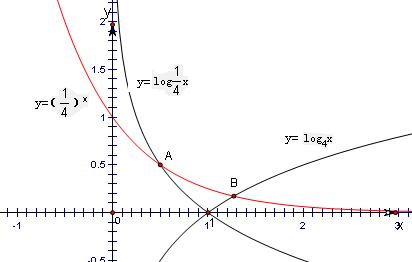

结合图象可得x₁=$\frac{1}{2}$，1＜x₂＜2，
∴$\frac{1}{2}$＜x₁x₂＜1，
故选：A．

点评 本题考查了根的存在性及根的个数判断，以及函数与方程的思想，解答关键是运用数形结合的思想，属于中档题．