
分析 (1)设P(x,y),利用两点间距离公式能求出点P的轨迹C的方程.
(2)求出N(1,0),当直线l的斜率不存在时,直线l的方程为x=1,不成立;当直线l的斜率成立时,设直线l的方程为y=k(x-1),联立$\left\{\begin{array}{l}{y=k(x-1)}\\{{x}^{2}+{y}^{2}-2x+8y+9=0}\end{array}\right.$,得(1+k2)x2-(2k2-8k+2)x+k2-8k+9=0,由此利用根的判别式、点到直线的距离公式、弦长公式能求出存在过点N的直线l,l与轨迹C相交于E、F两点,且使三角形${S_{△OEF}}=2\sqrt{2}$.
解答 解:(1)设P(x,y),
则${d}_{1}=\sqrt{(x-1)^{2}+{y}^{2}}$,d2=$\sqrt{({x}_{\;}-1)^{2}+(y+2)^{2}}$,
∵$\frac{d_1}{d_2}=\sqrt{2}$,
∴$\frac{\sqrt{(x-1)^{2}+{y}^{2}}}{\sqrt{(x-1)^{2}+(y+2)^{2}}}$=$\sqrt{2}$,
整理,得:x2+y2-2x+8y+9=0.
∴点P的轨迹C的方程为x2+y2-2x+8y+9=0.
(2)不存在过点N的直线l,l与轨迹C相交于E、F两点,且使三角形${S_{△OEF}}=2\sqrt{2}$.
理由如下:
∵点M(0,1)与点N关于直线x-y=0对称,∴N(1,0),
当直线l的斜率不存在时,直线l的方程为x=1,
联立$\left\{\begin{array}{l}{x=1}\\{{x}^{2}+{y}^{2}-2x+8y+9=0}\end{array}\right.$,得$\left\{\begin{array}{l}{x=1}\\{y=-2-2\sqrt{2}}\end{array}\right.$,或$\left\{\begin{array}{l}{x=1}\\{y=-2+2\sqrt{2}}\end{array}\right.$,
此时S△OEF=$\frac{1}{2}×1×4\sqrt{2}=2\sqrt{2}$,成立;
当直线l的斜率成立时,设直线l的方程为y=k(x-1),
联立$\left\{\begin{array}{l}{y=k(x-1)}\\{{x}^{2}+{y}^{2}-2x+8y+9=0}\end{array}\right.$,得(1+k2)x2-(2k2-8k+2)x+k2-8k+9=0,
△>0,设E(x1,y1),N(x2,y2),则${x}_{1}+{x}_{2}=\frac{2{k}^{2}-8k+2}{1+{k}^{2}}$,${x}_{1}{x}_{2}=\frac{{k}^{2}-8k+9}{1+{k}^{2}}$,
点O到直线y=k(x-1)的距离d=$\frac{|-k|}{\sqrt{{k}^{2}+1}}$=$\frac{|k|}{\sqrt{{k}^{2}+1}}$,
|EF|=$\sqrt{(1+{k}^{2})[(\frac{2{k}^{2}-8k+2}{1+{k}^{2}})^{2}-4×\frac{{k}^{2}-8k+9}{1+{k}^{2}}]}$=$\sqrt{\frac{32{k}^{2}-32}{1+{k}^{2}}}$,
∵${S_{△OEF}}=2\sqrt{2}$,
∴S△OEF=$\frac{1}{2}×|EF|×d$=$\frac{1}{2}×$$\sqrt{\frac{32{k}^{2}-32}{1+{k}^{2}}}$×$\frac{|k|}{\sqrt{{k}^{2}+1}}$=2$\sqrt{2}$,
整理,得3k2=-1,不成立,
综上,存在过点N的直线l:x=1,l与轨迹C相交于E、F两点,且使三角形${S_{△OEF}}=2\sqrt{2}$.
点评 本题考查两点距离公式的求法,考查满足条件的直线是否存在的判断与求法,是中档题,解题时要认真审题,注意根的判别式、点到直线的距离公式、弦长公式的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
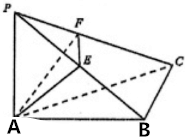 在三棱锥P-ABC中,已知PA⊥底面ABC,AB⊥BC,E,F分别是线段PB,PC上的动点.则下列说法错误的是( )
在三棱锥P-ABC中,已知PA⊥底面ABC,AB⊥BC,E,F分别是线段PB,PC上的动点.则下列说法错误的是( )| A. | 当AE⊥PB时,△AEF-定为直角三角形 | |
| B. | 当AF⊥PC时,△AEF-定为直角三角形 | |
| C. | 当EF∥平面ABC时,△AEF-定为直角三角形 | |
| D. | 当PC⊥平面AEF时,△AEF-定为直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com