
分析 (1)运用椭圆的定义,可得2a=$\sqrt{6}$,由离心率公式可得c的值,再由a,b,c的关系可得b的值,进而得到椭圆方程;
(2)设A(x1,y1),B(x2,y2),将直线方程y=-x-m代入椭圆方程,消去y,可得x的方程,运用判别式大于0和韦达定理,结合向量垂直的条件:数量积为0,化简整理,可得m的值.
解答 解:(1)由椭圆的定义可得2a=$\sqrt{6}$,
即a=$\frac{\sqrt{6}}{2}$,
由e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,可得c=$\frac{\sqrt{3}}{2}$,
则b=$\sqrt{{a}^{2}-{c}^{2}}$=$\frac{\sqrt{3}}{2}$,
可得椭圆的方程为$\frac{2{x}^{2}}{3}$+$\frac{4{y}^{2}}{3}$=1;
(2)设A(x1,y1),B(x2,y2),
将直线方程y=-x-m代入椭圆方程,可得
6x2+8mx+4m2-3=0,
由△=64m2-24(4m2-3)>0,
解得-$\frac{3}{2}$<m<$\frac{3}{2}$.
又x1+x2=-$\frac{4m}{3}$,x1x2=$\frac{4{m}^{2}-3}{6}$,
由OA⊥OB,可得$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,
即为x1x2+y1y2=0,
即x1x2+(-m-x1)(-m-x2)=0,
即有2x1x2+m2+m(x1+x2)=0,
可得$\frac{4{m}^{2}-3}{3}$+m2+m(-$\frac{4m}{3}$)=0,
解得m=±1,满足△>0.
则m的值为±1.
点评 本题考查椭圆的方程的求法,注意运用椭圆的定义和离心率公式,考查直线和椭圆的位置关系,注意运用联立直线方程和椭圆方程,运用判别式大于0和韦达定理,以及向量垂直的条件,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{3}{2}$,4) | B. | (-$\frac{3}{2}$,-4) | C. | ($\frac{3}{2}$,-4) | D. | (-3,-4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 曲线E上的所有点都是“好点” | |
| B. | 曲线E上仅有有限个点是“好点” | |
| C. | 曲线E上的所有点都不是“好点” | |
| D. | 曲线E上有无穷多个点(但不是所有的点)是“好点” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
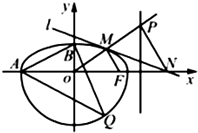 (文科)如图所示的封闭曲线C由曲线C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,y≥0)和曲线C2:x2+y2=r2(y<0)组成,已知曲线C1过点($\sqrt{3}$,$\frac{1}{2}$),离心率为$\frac{\sqrt{3}}{2}$,点A、B分别为曲线C与x轴、y轴的一个交点.
(文科)如图所示的封闭曲线C由曲线C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,y≥0)和曲线C2:x2+y2=r2(y<0)组成,已知曲线C1过点($\sqrt{3}$,$\frac{1}{2}$),离心率为$\frac{\sqrt{3}}{2}$,点A、B分别为曲线C与x轴、y轴的一个交点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
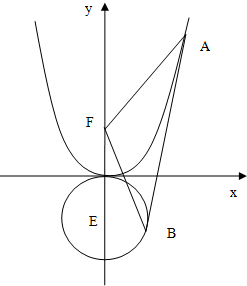 已知抛物线C:x2=2py(p>0),圆E:x2+(y+1)2=1,若直线L与抛物线C和圆E分别相切于点A,B(A,B不重合)
已知抛物线C:x2=2py(p>0),圆E:x2+(y+1)2=1,若直线L与抛物线C和圆E分别相切于点A,B(A,B不重合)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{3}$] | B. | (0,$\frac{1}{2}$] | C. | [-$\frac{1}{3}$,$\frac{1}{3}$] | D. | [-$\frac{1}{2}$,$\frac{1}{2}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com