
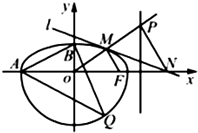
 ���Ŀƣ���ͼ��ʾ�ķ������C������C1��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0��y��0��������C2��x2+y2=r2��y��0����ɣ���֪����C1���㣨$\sqrt{3}$��$\frac{1}{2}$����������Ϊ$\frac{\sqrt{3}}{2}$����A��B�ֱ�Ϊ����C��x�ᡢy���һ�����㣮
���Ŀƣ���ͼ��ʾ�ķ������C������C1��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0��y��0��������C2��x2+y2=r2��y��0����ɣ���֪����C1���㣨$\sqrt{3}$��$\frac{1}{2}$����������Ϊ$\frac{\sqrt{3}}{2}$����A��B�ֱ�Ϊ����C��x�ᡢy���һ�����㣮���� ��I������C1���㣨$\sqrt{3}$��$\frac{1}{2}$����������Ϊ$\frac{\sqrt{3}}{2}$���ɵ�$\frac{3}{{a}^{2}}+\frac{1}{4{b}^{2}}$=1��$\frac{c}{a}=\frac{\sqrt{3}}{2}$����a2=b2+c2���������a��b���ɵ�����C1�ķ��̣��ɵ�A����A������C2�ϣ��ɵ�r��
��II��A��-2��0����B��0��1�������ýؾ�ʽ�ɵ�ֱ��AB�ķ��̣��������֪��������C2�ڵ�Q����������ֱ��ABƽ��ʱ����QAB�������������߷���Ϊ��x-2y+t=0����ֱ����Բ���е����ʿɵ�t������ƽ����֮��ľ��빫ʽ�ɵá�QAB��AB���ϵĸ�h�����ɵó�S��QAB�����ֵ=$\frac{1}{2}$|AB|h��
��III��������ɵã�k��0��F$��\sqrt{3}��0��$��N$��-\frac{m}{k}��0��$����M��x0��y0����ֱ�߷�������Բ����������Ϊ����1+4k2��x2+8kmx+4m2-4=0����ֱ��l������C1�����ڵ�M���ɵá�=0����m2=4k2+1�����ø���ϵ���Ĺ�ϵ�ɵ�M��kOM����P�����꣮�ɵ�$\overrightarrow{FM}$=��$\overrightarrow{NP}$������֤��MF��PN��
��� ��I���⣺������C1���㣨$\sqrt{3}$��$\frac{1}{2}$����������Ϊ$\frac{\sqrt{3}}{2}$��
��$\frac{3}{{a}^{2}}+\frac{1}{4{b}^{2}}$=1��$\frac{c}{a}=\frac{\sqrt{3}}{2}$����a2=b2+c2���������a=2��b=1��
�ɵ�����C1�ķ���Ϊ��$\frac{{x}^{2}}{4}$+y2=1����y��0����
�ɵ�A��-2��0�����ߵ�A������C2�ϣ���r=2���ɵ÷��̣�x2+y2=4��y��0����
��II���⣺A��-2��0����B��0��1�����ɵ�ֱ��AB�ķ��̣�$\frac{x}{-2}+\frac{y}{1}$=1����Ϊ��x-2y+2=0��
�������֪��������C2�ڵ�Q����������ֱ��ABƽ��ʱ����QAB��������
�����߷���Ϊ��x-2y+t=0����ֱ��Բ���е����ʿɵã�$\frac{|t|}{\sqrt{5}}$=2���ɿ�֪t��0�����t=-2$\sqrt{5}$��
��ʱ��QAB��AB���ϵĸ�h=$\frac{|2-��-2\sqrt{5}��|}{\sqrt{5}}$=2+$\frac{2\sqrt{5}}{5}$��
��S��QAB�����ֵ=$\frac{1}{2}$|AB|h=$\frac{1}{2}��\sqrt{5}$��$��2+\frac{2\sqrt{5}}{5}��$=$\sqrt{5}$+1�����QAB��������ֵΪ$\sqrt{5}$+1��
��III��֤����������ɵã�k��0��F$��\sqrt{3}��0��$��N$��-\frac{m}{k}��0��$��
���е�M��x0��y0������$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$����Ϊ����1+4k2��x2+8kmx+4m2-4=0��
��ֱ��l������C1�����ڵ�M�����=��8km��2-4��1+4k2����4m2-4��=0����m2=4k2+1��
x0=$\frac{1}{2}��$$��-\frac{8km}{1+4{k}^{2}}��$=-$\frac{4km}{1+4{k}^{2}}$��y0=kx0+m=$\frac{m}{1+4{k}^{2}}$��
��M$��-\frac{4km}{1+4{k}^{2}}��\frac{m}{1+4{k}^{2}}��$����M$��-\frac{4k}{m}��\frac{1}{m}��$����kOM=-$\frac{1}{4k}$��
��$P��\frac{4\sqrt{3}}{3}��-\frac{\sqrt{3}}{3k}��$��
��$\overrightarrow{FM}$=$��-\frac{4k}{m}-\sqrt{3}��\frac{1}{m}��$=$\frac{1}{m}$$��-4k-\sqrt{3}m��1��$��$\overrightarrow{NP}$=$��\frac{m}{k}+\frac{4\sqrt{3}}{3}��-\frac{\sqrt{3}}{3k}��$=-$\frac{\sqrt{3}}{3k}$$��-4k-\sqrt{3}m��1��$��
��$\overrightarrow{FM}$=-$\frac{\sqrt{3}k}{m}$$\overrightarrow{NP}$����MF��PN��
���� ���⿼������Բ��Բ�ı����̼������ʡ�ֱ����Բ�������⡢ֱ���ཻ���⡢������������㹫ʽ��ƽ����֮��ľ��빫ʽ����������������������������������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �����Φ£�m?����n?�£���m��n | |
| B�� | ��m��n?����m�֣�n�֣������ | |
| C�� | m��n������ֱ�ߣ���m�Φ���m�Φ£�n�Φ£�����Φ� | |
| D�� | �����֣�m������m�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
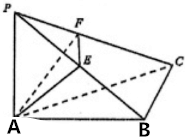 ������P-ABC�У���֪PA�͵���ABC��AB��BC��E��F�ֱ����߶�PB��PC�ϵĶ��㣮������˵��������ǣ�������
������P-ABC�У���֪PA�͵���ABC��AB��BC��E��F�ֱ����߶�PB��PC�ϵĶ��㣮������˵��������ǣ�������| A�� | ��AE��PBʱ����AEF-��Ϊֱ�������� | |
| B�� | ��AF��PCʱ����AEF-��Ϊֱ�������� | |
| C�� | ��EF��ƽ��ABCʱ����AEF-��Ϊֱ�������� | |
| D�� | ��PC��ƽ��AEFʱ����AEF-��Ϊֱ�������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
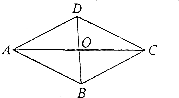 ������ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AB=5��AC=8����ͼ���������E�ڶԽ���AC�ϣ���DE=4��
������ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AB=5��AC=8����ͼ���������E�ڶԽ���AC�ϣ���DE=4���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com