
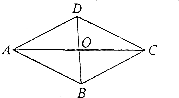
 ������ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AB=5��AC=8����ͼ���������E�ڶԽ���AC�ϣ���DE=4��
������ABCD�У��Խ���AC��BD�ཻ�ڵ�O��AB=5��AC=8����ͼ���������E�ڶԽ���AC�ϣ���DE=4������ ��1�����ù��ɶ������㣻
��2������ƽ����������������ļ�������ó����ۣ�
��� �⣺��1�����ı���ABCD�����Σ�
��AC��BD��OA=$\frac{1}{2}$AC=4��AD=AB=5��
��OD=$\sqrt{A{D}^{2}-O{A}^{2}}$=3��OE=$\sqrt{D{E}^{2}-O{D}^{2}}$=$\sqrt{7}$��
��AE=OA-OE=4-$\sqrt{7}$��AE=OA+OE=4+$\sqrt{7}$��
��2����$\overrightarrow{OC}=-\overrightarrow{OA}=-\overrightarrow{a}$��
��$\overrightarrow{BC}=\overrightarrow{OC}-\overrightarrow{OB}$=-$\overrightarrow{a}$-$\overrightarrow{b}$��
��$\overrightarrow{AD}=\overrightarrow{BC}$=-$\overrightarrow{a}$-$\overrightarrow{b}$��
��$\overrightarrow{AE}=\overrightarrow{AD}+\overrightarrow{DE}$=-$\overrightarrow{a}-\overrightarrow{b}$+$\overrightarrow{c}$��
���� ���⿼���˹��ɶ�����ƽ��������������ļ������壬���ڻ����⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
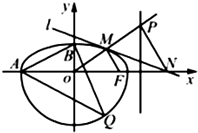 ���Ŀƣ���ͼ��ʾ�ķ������C������C1��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0��y��0��������C2��x2+y2=r2��y��0����ɣ���֪����C1���㣨$\sqrt{3}$��$\frac{1}{2}$����������Ϊ$\frac{\sqrt{3}}{2}$����A��B�ֱ�Ϊ����C��x�ᡢy���һ�����㣮
���Ŀƣ���ͼ��ʾ�ķ������C������C1��$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0��y��0��������C2��x2+y2=r2��y��0����ɣ���֪����C1���㣨$\sqrt{3}$��$\frac{1}{2}$����������Ϊ$\frac{\sqrt{3}}{2}$����A��B�ֱ�Ϊ����C��x�ᡢy���һ�����㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��$\frac{1}{3}$] | B�� | ��0��$\frac{1}{2}$] | C�� | [-$\frac{1}{3}$��$\frac{1}{3}$] | D�� | [-$\frac{1}{2}$��$\frac{1}{2}$] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��$\frac{1}{4}$] | B�� | ��$\frac{1}{4}$��$\frac{1}{2}$�� | C�� | ��0��$\frac{1}{2}$] | D�� | [$\frac{1}{4}$��$\frac{1}{2}$] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-2$\sqrt{2}$-$\frac{1}{2}$��2$\sqrt{2}$-$\frac{1}{2}$�� | B�� | [-2$\sqrt{2}$-$\frac{1}{2}$��2$\sqrt{2}$-$\frac{1}{2}$] | C�� | ��-$\sqrt{2}$-$\frac{1}{2}$��$\sqrt{2}$-$\frac{1}{2}$�� | D�� | [-$\sqrt{2}$-$\frac{1}{2}$��$\sqrt{2}$-$\frac{1}{2}$] |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com