
分析 对已知函数求导数,得y′=$\frac{1-x}{x}$(x>0),由导数的零点得到函数的极大值点为x=1,从而b=1,极大值c=-1,最后根据等比数列的性质可得ad=bc=-1.
解答 解:∵y=lnx-x,
∴y′=$\frac{1-x}{x}$(x>0).
当0<x<1时,f′(x)>0,函数在区间(0,1)为增函数;
当x>1时,f′(x)<0,函数在区间(1,+∞)为减函数.
∴当x=1时,函数有极大值为f(1)=-1,
∴b=1,c=-1,
又∵实数a,b,c,d成等比数列,
∴ad=bc=-1.
故答案为:-1.
点评 本题考查了利用导数工具研究函数的单调性,从而求出函数在其定义域上的极值,同时还考查了等比数列的性质,属于简单题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
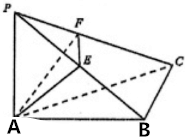 在三棱锥P-ABC中,已知PA⊥底面ABC,AB⊥BC,E,F分别是线段PB,PC上的动点.则下列说法错误的是( )
在三棱锥P-ABC中,已知PA⊥底面ABC,AB⊥BC,E,F分别是线段PB,PC上的动点.则下列说法错误的是( )| A. | 当AE⊥PB时,△AEF-定为直角三角形 | |
| B. | 当AF⊥PC时,△AEF-定为直角三角形 | |
| C. | 当EF∥平面ABC时,△AEF-定为直角三角形 | |
| D. | 当PC⊥平面AEF时,△AEF-定为直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com