练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    9．已知直线y=kx-3与圆x2+y2+2x-4y-4=0相交且经过圆心，则k=-5．

    分析 将圆的方程化为标准式，求出圆心坐标，代入直线方程求出k的值．

    解答 解：由x2+y2+2x-4y-4=0得，
    圆的标准方程是（x+1）2+（y-2）2=9，
    则圆心坐标是（-1，2），
    ∵直线y=kx-3与圆x2+y2+2x-4y-4=0相交且经过圆心，
    ∴2=-k-3，得k=-5，
    故答案为：-5．

    点评 本题考查圆的一般式方程，点、直线与圆的位置关系，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    13．已知直线l过点A（-2，-1），直线l的一个方向向量为（1，1），抛物线Γ的方程为y=ax2．
    （1）求直线l的方程；
    （2）若直线l与抛物线Γ交于B，C两点，且|BC|是|AB|和|AC|的等比中项，求抛物线Γ的方程；
    （3）设抛物线Γ的焦点为F，问：是否存在正整数a，使得抛物线Γ上至少有一点P，满足|PF|=|PA|，若存在，求出所有这样的正整数a的值；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．点P在曲线E：y=ex上，若存在过P的直线交曲线E于另一点A，交直线l：y=x-1于点B，且|PA|=|AB|，则称点P为“好点”，那么下列结论中正确的是（　　）
    A．曲线E上的所有点都是“好点”
    B．曲线E上仅有有限个点是“好点”
    C．曲线E上的所有点都不是“好点”
    D．曲线E上有无穷多个点（但不是所有的点）是“好点”

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

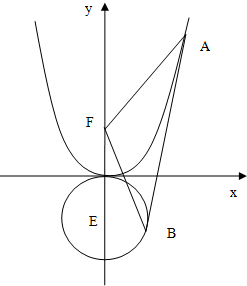    17．已知抛物线C：x2=2py（p＞0），圆E：x2+（y+1）2=1，若直线L与抛物线C和圆E分别相切于点A，B（A，B不重合）
    （Ⅰ）当p=1时，求直线L的方程；
    （Ⅱ）点F是抛物线C的焦点，若对于任意的p＞0，记△ABF面积为S，求$\frac{S}{{\sqrt{p+1}}}$的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．如图，已知点P是圆锥母线SA的中点，Q是底面圆周上的点，M是线段PQ的中点，当点Q在圆周上运动一周时，点M的轨迹是（　　）
    A．线段B．圆C．椭圆D．抛物线

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．已知实数a，b，c，d成等比数列，对于函数y=lnx-x，当x=b时取到极大值c，则ad等于-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．直线l：x-3y+4=0与圆（x-a）2+y2=5相交于A、B两点，设点P是直线l与x轴的交点，若点A恰好是线段PB的中点，则a=-4$±3\sqrt{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．若函数f（x）=x3-（4+log2a）x+2在（0，2]上有两个零点，则实数a的取值范围是（　　）
    A．$（\frac{1}{4}，\left.1]\right.$B．（$\frac{1}{2}$，2]C．[1，4）D．[2，8）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．已知等比数列{an}的前n项和是Sn，若S30=13S10，S10+S30=140，则S25的值为45$\sqrt{3}$-5或-45$\sqrt{3}$-5．

    查看答案和解析>>

    同步练习册答案