
分析 由已知得圆上点到原点距离d=5$\sqrt{2}$,从而|d-r|<$\sqrt{2}$|a|且d+r>$\sqrt{2}$|a|,由此能求出实数a的取值范围,即可求出圆心C到直线3x+4y=0距离d的取值范围.
解答 解:圆心(a,a)到原点的距离为$\sqrt{2}$|a|,半径r=10$\sqrt{2}$,
圆上点到原点距离为d,
∵圆(x-a)2+(y-a)2=200上总存在两个点到原点的距离为5$\sqrt{2}$,
∴d=5$\sqrt{2}$,
∴|d-r|<$\sqrt{2}$|a|且d+r>$\sqrt{2}$|a|
∴|$\frac{d-r}{\sqrt{2}}$|<|a|<$\frac{d+r}{\sqrt{2}}$,即5<|a|<15,
∴圆心C到直线3x+4y=0距离d=$\frac{|7a|}{\sqrt{9+16}}$∈(7,21).
故答案为:(7,21).
点评 本题考查了实数的取值范围与应用问题,解题时要认真审题,注意点到直线的距离公式的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{3}{2}$,4) | B. | (-$\frac{3}{2}$,-4) | C. | ($\frac{3}{2}$,-4) | D. | (-3,-4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
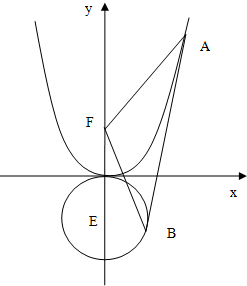 已知抛物线C:x2=2py(p>0),圆E:x2+(y+1)2=1,若直线L与抛物线C和圆E分别相切于点A,B(A,B不重合)
已知抛物线C:x2=2py(p>0),圆E:x2+(y+1)2=1,若直线L与抛物线C和圆E分别相切于点A,B(A,B不重合)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{1}{4},\left.1]\right.$ | B. | ($\frac{1}{2}$,2] | C. | [1,4) | D. | [2,8) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{3}$] | B. | (0,$\frac{1}{2}$] | C. | [-$\frac{1}{3}$,$\frac{1}{3}$] | D. | [-$\frac{1}{2}$,$\frac{1}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
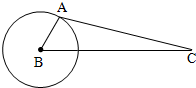 通讯卫星C在赤道上空3R(R为地球半径)的轨道上,它每24小时绕地球一周,所以它定位于赤道上某一点的上空.如果此点与某地A(北纬60°)在同一条子午在线,则在A观察此卫星的仰角的正切值为$\frac{3}{6}$.
通讯卫星C在赤道上空3R(R为地球半径)的轨道上,它每24小时绕地球一周,所以它定位于赤道上某一点的上空.如果此点与某地A(北纬60°)在同一条子午在线,则在A观察此卫星的仰角的正切值为$\frac{3}{6}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com