Question

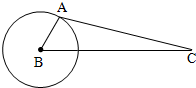
16．通讯卫星C在赤道上空3R（R为地球半径）的轨道上，它每24小时绕地球一周，所以它定位于赤道上某一点的上空．如果此点与某地A（北纬60°）在同一条子午在线，则在A观察此卫星的仰角的正切值为$\frac{3}{6}$．

Answer 1

分析 先过点A作圆的切线交BC于D，得到在A观察此卫星的仰角，再在三角形ABC中利用余弦定理求出角BAC的余弦值，再利用三角函数的同角公式得出其正切值，最后利用诱导公式即可求出仰角的正切值．

解答 解：过点A作圆的切线交BC于D，则在A观察此卫星的仰角就是∠CAD．
在三角形ABC中，由余弦定理得，AC²=AB²+BC²-2AB•BCcos60°=R²+（4R）²-2R•4R×$\frac{1}{2}$=13R²，
∴cos∠BAC=$\frac{A{B}^{2}+A{C}^{2}-B{C}^{2}}{2AB•AC}$=$\frac{{R}^{2}+13{R}^{2}-16{R}^{2}}{2R•\sqrt{13}R}=-\frac{1}{\sqrt{13}}$，
∴tan∠BAC=-2$\sqrt{3}$，
则在A观察此卫星的仰角的正切值为tan∠CAD=tan（∠BAC-90°）=-$\frac{1}{tan∠B∠AC}=\frac{\sqrt{3}}{6}$．
故答案为：$\frac{{\sqrt{3}}}{6}$．

点评 本题主要考查了与圆有关的比例线段，考查了切线的性质，以及解三角形等基本知识，属于基础题．