
分析 (1)由两切线垂直,可得|MP|=|MQ|=b,即有|OM|=$\sqrt{2}$b,即x02+y02=2b2,①由M在椭圆上,可得$\frac{{{x}_{0}}^{2}}{{a}^{2}}$+$\frac{{{y}_{0}}^{2}}{{b}^{2}}$=1,②,求出x02,y02,即可得到所求;
(2)M(x0,y0),由题意列出方程组求出$\frac{{b}^{2}}{{a}^{2}}$=$\frac{{{x}_{0}}^{2}-{{y}_{0}}^{2}}{2{{x}_{0}}^{2}}$,从而e=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\sqrt{\frac{{b}^{2}}{{{x}_{0}}^{2}}}$,由此能求出椭圆C2的离心率的取值范围.
解答 解:(1)点M(x0,y0),
由M向圆O:x2+y2=b2所引的两条切线MP,MQ互相垂直,
可得|MP|=|MQ|=b,
即有|OM|=$\sqrt{2}$b,即x02+y02=2b2,①
由M在椭圆上,可得$\frac{{{x}_{0}}^{2}}{{a}^{2}}$+$\frac{{{y}_{0}}^{2}}{{b}^{2}}$=1,②
由①②解得x02=$\frac{{a}^{2}{b}^{2}}{{a}^{2}-{b}^{2}}$,
y02=$\frac{{a}^{2}{b}^{2}-2{b}^{4}}{{a}^{2}-{b}^{2}}$,
则x02-y02=$\frac{2{b}^{4}}{{a}^{2}-{b}^{2}}$;
(2)由x02+y02=2b2,①
$\frac{{{x}_{0}}^{2}}{{a}^{2}}$+$\frac{{{y}_{0}}^{2}}{{b}^{2}}$=1,②
∴b2x02=$\frac{{{x}_{0}}^{2}+{{y}_{0}}^{2}}{2}$a2-a2y02=a2•$\frac{{{x}_{0}}^{2}-{{y}_{0}}^{2}}{2}$,
∴$\frac{{b}^{2}}{{a}^{2}}$=$\frac{{{x}_{0}}^{2}-{{y}_{0}}^{2}}{2{{x}_{0}}^{2}}$,
∴e=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\sqrt{\frac{2{{x}_{0}}^{2}-{{x}_{0}}^{2}+{{y}_{0}}^{2}}{2{{x}_{0}}^{2}}}$=$\sqrt{\frac{{{x}_{0}}^{2}+{{y}_{0}}^{2}}{2{{x}_{0}}^{2}}}$=$\sqrt{\frac{{b}^{2}}{{{x}_{0}}^{2}}}$,
∵-a≤x0≤a,
∴x0=b时,emax→$\sqrt{2-1}$=1,
x0=a时,emin=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\sqrt{\frac{{b}^{2}}{{a}^{2}}}$,
∴$\frac{{b}^{2}}{{a}^{2}}$=$\frac{1}{2}$,
∴emin=$\sqrt{1-\frac{1}{2}}$=$\frac{\sqrt{2}}{2}$,
又0<e<1,
∴椭圆C的离心率的取值范围是[$\frac{\sqrt{2}}{2}$,1).
点评 本题主要考查椭圆的离心率的取值范围的求法,是中档题,解题时要认真审题,注意椭圆性质的灵活运用.


科目:高中数学 来源: 题型:选择题
| A. | $(\frac{1}{4},\left.1]\right.$ | B. | ($\frac{1}{2}$,2] | C. | [1,4) | D. | [2,8) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
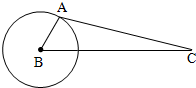 通讯卫星C在赤道上空3R(R为地球半径)的轨道上,它每24小时绕地球一周,所以它定位于赤道上某一点的上空.如果此点与某地A(北纬60°)在同一条子午在线,则在A观察此卫星的仰角的正切值为$\frac{3}{6}$.
通讯卫星C在赤道上空3R(R为地球半径)的轨道上,它每24小时绕地球一周,所以它定位于赤道上某一点的上空.如果此点与某地A(北纬60°)在同一条子午在线,则在A观察此卫星的仰角的正切值为$\frac{3}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com