
| A. | (-1,1) | B. | (1,$\frac{π}{2}$) | C. | (0,$\frac{π}{2}$) | D. | (-1,$\frac{π}{2}$) |
分析 令g(x)=cosx+xsinx,x∈(-π,π),分析直线y=a与g(x)=cosx+xsinx的图象有四个交点a的取值范围,可得答案.
解答 解:令g(x)=cosx+xsinx,x∈(-π,π),
则g′(x)=xcosx,x∈(-π,π),
令g′(x)<0,则x∈(-$\frac{π}{2}$,0)∪($\frac{π}{2}$,π),令g′(x)>0,则x∈(-π,-$\frac{π}{2}$)∪(0,$\frac{π}{2}$),
故g(x)在(-π,-$\frac{π}{2}$)上为增函数,在(-$\frac{π}{2}$,0)上为减函数,在(0,$\frac{π}{2}$)上为增函数,在($\frac{π}{2}$,π)上为减函数,
故g(x)在x=-$\frac{π}{2}$和x=$\frac{π}{2}$取极大值$\frac{π}{2}$,在x=0时取极小值1,
又由g(-π)=g(π)=-1,
故当a∈(1,$\frac{π}{2}$)时,直线y=a与g(x)=cosx+xsinx的图象有四个交点,
即函数f(x)=cosx+xsinx-a,x∈(-π,π)有4个零点,
故选:B.
点评 本题考查的知识点是利用导数研究函数的极值,函数的零点,难度中档.


科目:高中数学 来源: 题型:解答题
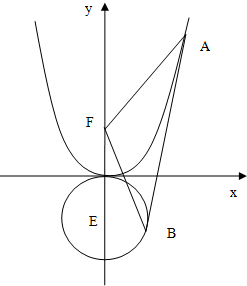 已知抛物线C:x2=2py(p>0),圆E:x2+(y+1)2=1,若直线L与抛物线C和圆E分别相切于点A,B(A,B不重合)
已知抛物线C:x2=2py(p>0),圆E:x2+(y+1)2=1,若直线L与抛物线C和圆E分别相切于点A,B(A,B不重合)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{1}{4},\left.1]\right.$ | B. | ($\frac{1}{2}$,2] | C. | [1,4) | D. | [2,8) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{3}$] | B. | (0,$\frac{1}{2}$] | C. | [-$\frac{1}{3}$,$\frac{1}{3}$] | D. | [-$\frac{1}{2}$,$\frac{1}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
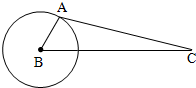 通讯卫星C在赤道上空3R(R为地球半径)的轨道上,它每24小时绕地球一周,所以它定位于赤道上某一点的上空.如果此点与某地A(北纬60°)在同一条子午在线,则在A观察此卫星的仰角的正切值为$\frac{3}{6}$.
通讯卫星C在赤道上空3R(R为地球半径)的轨道上,它每24小时绕地球一周,所以它定位于赤道上某一点的上空.如果此点与某地A(北纬60°)在同一条子午在线,则在A观察此卫星的仰角的正切值为$\frac{3}{6}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com