
分析 若$\frac{1}{1-{2}^{a}}$+$\frac{1}{1-{2}^{b+1}}$=1,去分母可得2a+b+1=1,进而得到答案.
解答 解:∵$\frac{1}{1-{2}^{a}}$+$\frac{1}{1-{2}^{b+1}}$=1,
∴$\frac{2-{2}^{a}-{2}^{b+1}}{(1-{2}^{a})(1-{2}^{b+1})}$=1,
∴2-2a-2b+1=1-2a-2b+1+2a+b+1,
∴2a+b+1=1,
∴a+b+1=0,
∴a+b=-1,
故答案为:-1
点评 本题考查的知识点是分式方程的解法,指数方程的解法,将原方程转化为整式方程是解答的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知圆F1:(x+1)2+y2=r2与F2:(x-1)2+y2=(4-r)2(0<r<4)的公共点的轨迹为曲线E
已知圆F1:(x+1)2+y2=r2与F2:(x-1)2+y2=(4-r)2(0<r<4)的公共点的轨迹为曲线E查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
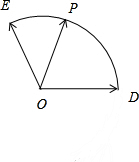 如图,若$\overrightarrow{a}$=$\overrightarrow{OD}$,$\overrightarrow{b}$=$\overrightarrow{OE}$,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为120°,|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1,点P是以点O为圆心的圆弧$\widehat{DE}$上一动点,设$\overrightarrow{OP}$=x$\overrightarrow{OD}$+y$\overrightarrow{OE}$(x,y∈R),求x+y的最大值.
如图,若$\overrightarrow{a}$=$\overrightarrow{OD}$,$\overrightarrow{b}$=$\overrightarrow{OE}$,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为120°,|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1,点P是以点O为圆心的圆弧$\widehat{DE}$上一动点,设$\overrightarrow{OP}$=x$\overrightarrow{OD}$+y$\overrightarrow{OE}$(x,y∈R),求x+y的最大值.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | (1,$\frac{π}{2}$) | C. | (0,$\frac{π}{2}$) | D. | (-1,$\frac{π}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com