
分析 x=1时,正三棱锥S-ABC变成正四面体.如图所示,取BC的中点D,SA的中点E,连接SD,AD,DE.利用等边三角形的性质可得:SD=AD=$\frac{\sqrt{3}}{2}$,又SE=EA=$\frac{1}{2}$,可得DE⊥SA,DE⊥BC.因此DE为SA与BC的距离d,利用勾股定理即可得出.
解答 解:x=1时,正三棱锥S-ABC变成正四面体.如图所示,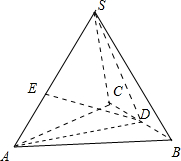
取BC的中点D,SA的中点E,连接SD,AD,DE.
∵△ABC与△SBC是边长为1的等边三角形,
∴SD=AD=$\frac{\sqrt{3}}{2}$,又SE=EA=$\frac{1}{2}$,
∴DE⊥SA,同理可得DE⊥BC.
∴DE为SA与BC的距离d,
d=DE=$\sqrt{(\frac{\sqrt{3}}{2})^{2}-(\frac{1}{2})^{2}}$=$\frac{\sqrt{2}}{2}$.
∴$\underset{lim}{x→1}$d=$\frac{\sqrt{2}}{2}$.
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题考查了正四面体的性质、等边三角形与等腰三角形的性质、异面直线之间的距离、勾股定理、极限的性质,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 曲线E上的所有点都是“好点” | |
| B. | 曲线E上仅有有限个点是“好点” | |
| C. | 曲线E上的所有点都不是“好点” | |
| D. | 曲线E上有无穷多个点(但不是所有的点)是“好点” |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{1}{4},\left.1]\right.$ | B. | ($\frac{1}{2}$,2] | C. | [1,4) | D. | [2,8) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{3}$] | B. | (0,$\frac{1}{2}$] | C. | [-$\frac{1}{3}$,$\frac{1}{3}$] | D. | [-$\frac{1}{2}$,$\frac{1}{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com