
分析 由圆的方程求出圆心和半径,根据点到直线距离公式求出圆心到直线的距离,
(1)由直线与圆相交的条件列出不等式,求出k的取值范围;
(2)由直线与圆相切的条件列出方程,求出k的值;
(3)由直线与圆相离的条件列出不等式,求出k的取值范围.
解答 解:由题意得,圆的半径为1、圆心坐标是(0,0),
∴圆心(0,0)到直线y=kx+2距离d=$\frac{2}{\sqrt{{k}^{2}+1}}$,
(1)∵直线y=kx+2与圆x2+y2=1相交,
∴$\frac{2}{\sqrt{{k}^{2}+1}}$<1,解得k<$-\sqrt{3}$或k>$\sqrt{3}$,
则k的取值范围是$(-∞,-\sqrt{3})∪(\sqrt{3},+∞)$;
(2)∵直线y=kx+2与圆x2+y2=1相切,
∴$\frac{2}{\sqrt{{k}^{2}+1}}$=1,解得k<$-\sqrt{3}$或k>$\sqrt{3}$,
则k的值是$-\sqrt{3}$或$\sqrt{3}$;
(3)∵直线y=kx+2与圆x2+y2=1相离,
∴$\frac{2}{\sqrt{{k}^{2}+1}}$>1,解得$-\sqrt{3}$<k<$\sqrt{3}$,
则k的取值范围是($-\sqrt{3},\sqrt{3}$).
点评 本题考查直线和圆的位置关系的判断方法:几何法,及点到直线的距离公式的应用,考查化简、计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知圆F1:(x+1)2+y2=r2与F2:(x-1)2+y2=(4-r)2(0<r<4)的公共点的轨迹为曲线E
已知圆F1:(x+1)2+y2=r2与F2:(x-1)2+y2=(4-r)2(0<r<4)的公共点的轨迹为曲线E查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
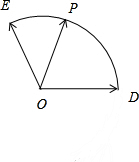 如图,若$\overrightarrow{a}$=$\overrightarrow{OD}$,$\overrightarrow{b}$=$\overrightarrow{OE}$,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为120°,|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1,点P是以点O为圆心的圆弧$\widehat{DE}$上一动点,设$\overrightarrow{OP}$=x$\overrightarrow{OD}$+y$\overrightarrow{OE}$(x,y∈R),求x+y的最大值.
如图,若$\overrightarrow{a}$=$\overrightarrow{OD}$,$\overrightarrow{b}$=$\overrightarrow{OE}$,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为120°,|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1,点P是以点O为圆心的圆弧$\widehat{DE}$上一动点,设$\overrightarrow{OP}$=x$\overrightarrow{OD}$+y$\overrightarrow{OE}$(x,y∈R),求x+y的最大值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com