
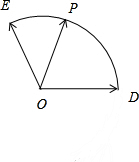
 »γΆΦΘ§»τ$\overrightarrow{a}$=$\overrightarrow{OD}$Θ§$\overrightarrow{b}$=$\overrightarrow{OE}$Θ§$\overrightarrow{a}$”κ$\overrightarrow{b}$ΒΡΦ–Ϋ«ΈΣ120ΓψΘ§|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1Θ§ΒψP «“‘ΒψOΈΣ‘≤–ΡΒΡ‘≤ΜΓ$\widehat{DE}$…œ“ΜΕ·ΒψΘ§…η$\overrightarrow{OP}$=x$\overrightarrow{OD}$+y$\overrightarrow{OE}$Θ®xΘ§yΓ RΘ©Θ§«σx+yΒΡΉν¥σ÷ΒΘ°
»γΆΦΘ§»τ$\overrightarrow{a}$=$\overrightarrow{OD}$Θ§$\overrightarrow{b}$=$\overrightarrow{OE}$Θ§$\overrightarrow{a}$”κ$\overrightarrow{b}$ΒΡΦ–Ϋ«ΈΣ120ΓψΘ§|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1Θ§ΒψP «“‘ΒψOΈΣ‘≤–ΡΒΡ‘≤ΜΓ$\widehat{DE}$…œ“ΜΕ·ΒψΘ§…η$\overrightarrow{OP}$=x$\overrightarrow{OD}$+y$\overrightarrow{OE}$Θ®xΘ§yΓ RΘ©Θ§«σx+yΒΡΉν¥σ÷ΒΘ° Ζ÷Έω “‘OPΈΣΕ‘Ϋ«œΏΉς≥ωΤΫ––ΥΡ±Ώ–ΈΘ§…ηΓœPOD=ΠΝΘ§άϊ”Ο’ΐœ“Ε®άμ«σ≥ωΤΫ––ΥΡ±Ώ–ΈΒΡ±Ώ≥ΛΒΟ≥ωxΘ§yΘ§ΗυΨί»ΐΫ«Κ· ΐΒΡ–‘÷ ΦΑΠΝΒΡΖΕΈßΒΟ≥ωx+yΒΡΉν¥σ÷ΒΘ°
Ϋβ¥π ΫβΘΚ “‘ODΘ§OEΈΣΝΎ±ΏΘ§“‘OPΈΣΕ‘Ϋ«œΏΉςΤΫ––ΥΡ±Ώ–ΈOMPNΘ§
“‘ODΘ§OEΈΣΝΎ±ΏΘ§“‘OPΈΣΕ‘Ϋ«œΏΉςΤΫ––ΥΡ±Ώ–ΈOMPNΘ§
‘ρ$\overrightarrow{OP}=\overrightarrow{OM}+\overrightarrow{ON}$Θ§
…ηΓœPOD=ΠΝΘ§‘ρΓœOMP=180Γψ-ΓœDOE=60ΓψΘ§ΓœOPM=120Γψ-ΠΝΘ°
‘ΎΓςOPM÷–Θ§”…’ΐœ“Ε®άμΒΟ$\frac{OP}{sin60Γψ}=\frac{OM}{sinΘ®120Γψ-ΠΝΘ©}=\frac{PM}{sinΠΝ}$=$\frac{1}{\frac{\sqrt{3}}{2}}=\frac{2\sqrt{3}}{3}$Θ§
Γύ|OM|=$\frac{2\sqrt{3}}{3}$sinΘ®120Γψ-ΠΝΘ©=$\frac{2\sqrt{3}}{3}$Θ®$\frac{\sqrt{3}}{2}$cosΠΝ+$\frac{1}{2}$sinΠΝΘ©Θ§|PM|=$\frac{2\sqrt{3}}{3}$sinΠΝΘ°
ΓΏOD=OE=1Θ§
Γύ$\overrightarrow{OM}=OM•\overrightarrow{OD}$Θ§$\overrightarrow{ON}=PM•\overrightarrow{OE}$Θ§
”÷$\overrightarrow{OP}=x\overrightarrow{OD}+y\overrightarrow{OE}$Θ§
Γύx=cosΠΝ+$\frac{\sqrt{3}}{3}$sinΠΝΘ§y=$\frac{2\sqrt{3}}{3}$sinΠΝΘ°
Γύx+y=cosΠΝ+$\sqrt{3}$sinΠΝ=2sinΘ®ΠΝ+30ΓψΘ©Θ§
ΓΏ0ΓψΓήΠΝΓή120ΓψΘ§
ΓύΒ±ΠΝ+30Γψ=90ΓψΦ¥ΠΝ=60Γψ ±x+y»ΓΒΟΉν¥σ÷Β2Θ°
Γύx+yΒΡΉν¥σ÷ΒΈΣ2Θ°
ΒψΤά ±ΨΧβΩΦ≤ιΝΥΤΫΟφœρΝΩΒΡΜυ±ΨΕ®άμΘ§’ΐœ“Ε®άμΘ§»ΐΫ«Κ· ΐΒΡΜ·Φρ”κ«σ÷ΒΘ§ τ”Ύ÷–ΒΒΧβΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | -1 | BΘ° | 3 | CΘ° | -$\frac{1}{3}$ | DΘ° | $\frac{1}{3}$ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | [$\frac{3}{2}$Θ§5Θ© | BΘ° | [$\frac{3}{2}$Θ§3] | CΘ° | [3Θ§5Θ© | DΘ° | [3Θ§5] |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
 »γΆΦΘ§“―÷Σ|$\overrightarrow{OA}$|=2Θ§|$\overrightarrow{OB}$|=2$\sqrt{3}$Θ§$\overrightarrow{OA}$•$\overrightarrow{OB}$=0ΒψC‘ΎœΏΕΈAB…œΘ§ΓœAOC=30ΓψΘ§”Ο$\overrightarrow{OA}$ΚΆ$\overrightarrow{OB}$ά¥±μ ΨœρΝΩ$\overrightarrow{OC}$Θ§‘ρ$\overrightarrow{OC}$Β»”Ύ$\frac{3}{4}\overrightarrow{OA}$+$\frac{1}{4}\overrightarrow{OB}$Θ°
»γΆΦΘ§“―÷Σ|$\overrightarrow{OA}$|=2Θ§|$\overrightarrow{OB}$|=2$\sqrt{3}$Θ§$\overrightarrow{OA}$•$\overrightarrow{OB}$=0ΒψC‘ΎœΏΕΈAB…œΘ§ΓœAOC=30ΓψΘ§”Ο$\overrightarrow{OA}$ΚΆ$\overrightarrow{OB}$ά¥±μ ΨœρΝΩ$\overrightarrow{OC}$Θ§‘ρ$\overrightarrow{OC}$Β»”Ύ$\frac{3}{4}\overrightarrow{OA}$+$\frac{1}{4}\overrightarrow{OB}$Θ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ

| AΘ° | PD?ΤΫΟφABC | BΘ° | PDΓΆΤΫΟφABC | ||
| CΘ° | PD”κΤΫΟφABCœύΫΜΒΪ≤Μ¥Ι÷± | DΘ° | PDΓΈΤΫΟφABC |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com