
分析 由题意得到$\left\{\begin{array}{l}x+10=y-2\\ 3x+20=y\end{array}\right.$,从而求出x,y,再由逆矩阵公式求出矩阵M的逆矩阵,由此能求出${M^{-1}}[{\begin{array}{l}x\\ y\end{array}}]$.
解答 解:∵点P(x,5)在矩阵M=$[{\begin{array}{l}1&2\\ 3&4\end{array}}]$对应的变换下得到点Q(y-2,y),
∴依题意,$[{\begin{array}{l}1&2\\ 3&4\end{array}}]$$[{\begin{array}{l}x\\ 5\end{array}}]$=$[{\begin{array}{l}{y-2}\\ y\end{array}}]$,即$\left\{\begin{array}{l}x+10=y-2\\ 3x+20=y\end{array}\right.$解得$\left\{\begin{array}{l}x=-4\\ y=8\end{array}\right.$
由逆矩阵公式知,矩阵M=$[{\begin{array}{l}1&2\\ 3&4\end{array}}]$的逆矩阵${M^{-1}}=[{\begin{array}{l}{-2}&1\\{\frac{3}{2}}&{-\frac{1}{2}}\end{array}}]$,(8分)
∴${M^{-1}}[{\begin{array}{l}x\\ y\end{array}}]$=$[{\begin{array}{l}{-2}&1\\{\frac{3}{2}}&{-\frac{1}{2}}\end{array}}]$$[{\begin{array}{l}{-4}\\ 8\end{array}}]$=$[{\begin{array}{l}{16}\\{-10}\end{array}}]$.(10分)
点评 本题考查矩阵变换的应用,是中档题,解题时要认真审题,注意逆矩阵公式的合理运用.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:选择题
 一矩形的一边在x轴上,另两个顶点在函数y=$\frac{x}{{1+{x^2}}}$(x>0)的图象上,如图,则此矩形绕x轴旋转而成的几何体的体积的最大值是( )
一矩形的一边在x轴上,另两个顶点在函数y=$\frac{x}{{1+{x^2}}}$(x>0)的图象上,如图,则此矩形绕x轴旋转而成的几何体的体积的最大值是( )| A. | π | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
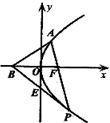 已知抛物线C:y2=2px(p≠0)的焦点F在直线2x+y-2=0上.
已知抛物线C:y2=2px(p≠0)的焦点F在直线2x+y-2=0上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知圆F1:(x+1)2+y2=r2与F2:(x-1)2+y2=(4-r)2(0<r<4)的公共点的轨迹为曲线E
已知圆F1:(x+1)2+y2=r2与F2:(x-1)2+y2=(4-r)2(0<r<4)的公共点的轨迹为曲线E查看答案和解析>>
科目:高中数学 来源: 题型:解答题
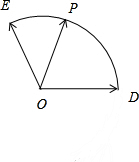 如图,若$\overrightarrow{a}$=$\overrightarrow{OD}$,$\overrightarrow{b}$=$\overrightarrow{OE}$,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为120°,|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1,点P是以点O为圆心的圆弧$\widehat{DE}$上一动点,设$\overrightarrow{OP}$=x$\overrightarrow{OD}$+y$\overrightarrow{OE}$(x,y∈R),求x+y的最大值.
如图,若$\overrightarrow{a}$=$\overrightarrow{OD}$,$\overrightarrow{b}$=$\overrightarrow{OE}$,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为120°,|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1,点P是以点O为圆心的圆弧$\widehat{DE}$上一动点,设$\overrightarrow{OP}$=x$\overrightarrow{OD}$+y$\overrightarrow{OE}$(x,y∈R),求x+y的最大值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设点P为圆C1:x2+y2=2上的动点,过点P作x轴的垂线,垂足为Q,点M满足$\sqrt{2}$$\overrightarrow{MQ}$=$\overrightarrow{PQ}$.
设点P为圆C1:x2+y2=2上的动点,过点P作x轴的垂线,垂足为Q,点M满足$\sqrt{2}$$\overrightarrow{MQ}$=$\overrightarrow{PQ}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com