
 设点P为圆C1:x2+y2=2上的动点,过点P作x轴的垂线,垂足为Q,点M满足$\sqrt{2}$$\overrightarrow{MQ}$=$\overrightarrow{PQ}$.
设点P为圆C1:x2+y2=2上的动点,过点P作x轴的垂线,垂足为Q,点M满足$\sqrt{2}$$\overrightarrow{MQ}$=$\overrightarrow{PQ}$.分析 (1)设P(x0,y0),M(x,y),通过$\sqrt{2}\overrightarrow{MQ}=\overrightarrow{PQ}$,转化求解,点M的轨迹C2的方程.
(2)设点T(2,t),则直线AB的方程为2x+ty=2,求出|AB|,设C(x1,y1),D(x2,y2),联立直线与椭圆的方程,利用弦长公式,求解$\frac{{|{CD}|}}{{|{AB}|}}$的表达式,通过函数的导数求解函数的最值即可.
解答 解:(1)设P(x0,y0),M(x,y),则
由$\sqrt{2}\overrightarrow{MQ}=\overrightarrow{PQ}$得到:$\left\{\begin{array}{l}{x_0}=x\\{y_0}=\sqrt{2}y\end{array}\right.$代入${x_0}^2+{y_0}^2=2$
得到:$\frac{x^2}{2}+{y^2}=1$,
所以,点M的轨迹C2的方程为$\frac{x^2}{2}+{y^2}=1$.
(2)设点T(2,t),则直线AB的方程为2x+ty=2,$|{AB}|=2\sqrt{\frac{{2{t^2}+4}}{{{t^2}+4}}}$,
又设C(x1,y1),D(x2,y2),则$\left\{\begin{array}{l}2x+ty=2\\{x^2}+2{y^2}=2\end{array}\right.$,得(t2+8)y2-4ty-4=0,
于是,${y_1}+{y_2}=\frac{4t}{{{t^2}+8}},{y_1}{y_2}=\frac{-4}{{{t^2}+8}},△>0$,
所以,$|{CD}|=\frac{{2\sqrt{{t^2}+4}•\sqrt{2{t^2}+8}}}{{{t^2}+8}}$,于是$\frac{{|{AB}|}}{{|{CD}|}}=\frac{{({{t^2}+8})\sqrt{{t^2}+2}}}{{({{t^2}+4})\sqrt{{t^2}+4}}}$,
令t2+4=s≥4,则$\frac{{|{AB}|}}{{|{CD}|}}=\frac{{({s+2})\sqrt{s-2}}}{{s\sqrt{s}}}=\sqrt{\frac{{{s^3}+6{s^2}-32}}{s^3}}=\sqrt{1+\frac{6}{s}-\frac{32}{s^3}}$
令$m=\frac{1}{s}∈({0,\frac{1}{4}}]$,于是$\frac{{|{AB}|}}{{|{CD}|}}=\sqrt{1+6m-32{m^3}}$,
设f(m)=-32m3+6m+1,f'(m)=-96m2+6,$-96{m^2}+6=0⇒m=±\frac{1}{4}$
所以,f(m)在$({0,\frac{1}{4}}]$单调递增,故$f(m)∈({1,\sqrt{2}}]$,
所以,$\frac{{|{CD}|}}{{|{AB}|}}∈[{\frac{{\sqrt{2}}}{2},1})$.
点评 本题考查轨迹方程的求法,直线与椭圆的位置关系的综合应用,构造法以及函数的导数的应用,考查转化思想以及计算能力.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{3}{2}$,5) | B. | [$\frac{3}{2}$,3] | C. | [3,5) | D. | [3,5] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,已知|$\overrightarrow{OA}$|=2,|$\overrightarrow{OB}$|=2$\sqrt{3}$,$\overrightarrow{OA}$•$\overrightarrow{OB}$=0点C在线段AB上,∠AOC=30°,用$\overrightarrow{OA}$和$\overrightarrow{OB}$来表示向量$\overrightarrow{OC}$,则$\overrightarrow{OC}$等于$\frac{3}{4}\overrightarrow{OA}$+$\frac{1}{4}\overrightarrow{OB}$.
如图,已知|$\overrightarrow{OA}$|=2,|$\overrightarrow{OB}$|=2$\sqrt{3}$,$\overrightarrow{OA}$•$\overrightarrow{OB}$=0点C在线段AB上,∠AOC=30°,用$\overrightarrow{OA}$和$\overrightarrow{OB}$来表示向量$\overrightarrow{OC}$,则$\overrightarrow{OC}$等于$\frac{3}{4}\overrightarrow{OA}$+$\frac{1}{4}\overrightarrow{OB}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
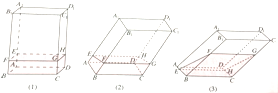 如图,透明塑料制成的长方体ABCD-A′B′C′D内灌进一些水,固定容器底面一边BC与地面上,再将容器倾斜.随着倾斜度的不同,有下面四个命题:
如图,透明塑料制成的长方体ABCD-A′B′C′D内灌进一些水,固定容器底面一边BC与地面上,再将容器倾斜.随着倾斜度的不同,有下面四个命题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | PD?平面ABC | B. | PD⊥平面ABC | ||
| C. | PD与平面ABC相交但不垂直 | D. | PD∥平面ABC |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com