
 如图,已知|$\overrightarrow{OA}$|=2,|$\overrightarrow{OB}$|=2$\sqrt{3}$,$\overrightarrow{OA}$•$\overrightarrow{OB}$=0点C在线段AB上,∠AOC=30°,用$\overrightarrow{OA}$和$\overrightarrow{OB}$来表示向量$\overrightarrow{OC}$,则$\overrightarrow{OC}$等于$\frac{3}{4}\overrightarrow{OA}$+$\frac{1}{4}\overrightarrow{OB}$.
如图,已知|$\overrightarrow{OA}$|=2,|$\overrightarrow{OB}$|=2$\sqrt{3}$,$\overrightarrow{OA}$•$\overrightarrow{OB}$=0点C在线段AB上,∠AOC=30°,用$\overrightarrow{OA}$和$\overrightarrow{OB}$来表示向量$\overrightarrow{OC}$,则$\overrightarrow{OC}$等于$\frac{3}{4}\overrightarrow{OA}$+$\frac{1}{4}\overrightarrow{OB}$. 分析 利用三角形知识求出AC,AB,用$\overrightarrow{OA},\overrightarrow{OB}$表示出$\overrightarrow{AC}$,于是$\overrightarrow{OC}=\overrightarrow{OA}+\overrightarrow{AC}$.
解答 解:∵$\overrightarrow{OA}•\overrightarrow{OB}=0$,∴OA⊥OB.
∵OA=2,OB=2$\sqrt{3}$,
∴|AB|=$\sqrt{O{A}^{2}+O{B}^{2}}$=4,∠A=60°,∠B=30°.
∵∠AOC=30°,
∴OC⊥AB,
∴AC=$\frac{1}{2}OA=1$,
∴$\overrightarrow{AC}=\frac{1}{4}\overrightarrow{AB}$=$\frac{1}{4}$$\overrightarrow{OB}$-$\frac{1}{4}$$\overrightarrow{OA}$,
∴$\overrightarrow{OC}=\overrightarrow{OA}+\overrightarrow{AC}$=$\frac{3}{4}\overrightarrow{OA}$+$\frac{1}{4}\overrightarrow{OB}$.
故答案为:$\frac{3}{4}\overrightarrow{OA}$+$\frac{1}{4}\overrightarrow{OB}$.
点评 本题考查了平面向量的线性运算的几何意义,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
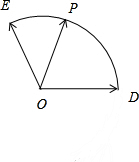 如图,若$\overrightarrow{a}$=$\overrightarrow{OD}$,$\overrightarrow{b}$=$\overrightarrow{OE}$,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为120°,|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1,点P是以点O为圆心的圆弧$\widehat{DE}$上一动点,设$\overrightarrow{OP}$=x$\overrightarrow{OD}$+y$\overrightarrow{OE}$(x,y∈R),求x+y的最大值.
如图,若$\overrightarrow{a}$=$\overrightarrow{OD}$,$\overrightarrow{b}$=$\overrightarrow{OE}$,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为120°,|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1,点P是以点O为圆心的圆弧$\widehat{DE}$上一动点,设$\overrightarrow{OP}$=x$\overrightarrow{OD}$+y$\overrightarrow{OE}$(x,y∈R),求x+y的最大值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设点P为圆C1:x2+y2=2上的动点,过点P作x轴的垂线,垂足为Q,点M满足$\sqrt{2}$$\overrightarrow{MQ}$=$\overrightarrow{PQ}$.
设点P为圆C1:x2+y2=2上的动点,过点P作x轴的垂线,垂足为Q,点M满足$\sqrt{2}$$\overrightarrow{MQ}$=$\overrightarrow{PQ}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com