
分析 设AB的中点为P,依题意,|MP|=$\frac{1}{2}$|AB|,|MP|最小时,弦AB长度最小,M、O、P三点共线时,满足题意,从而可得答案.
解答 解:设AB的中点为P,依题意,|MP|=$\frac{1}{2}$|AB|,|MP|最小时,弦AB长度最小,M、O、P三点共线时,满足题意,
此时△MAB是等腰直角三角形,MB∥x轴.
y=1时,x=±$\sqrt{3}$,∴|MB|=$\sqrt{3}$-1,
∴弦AB长度最小值为$\sqrt{2}$|MB|=$\sqrt{6}$-$\sqrt{2}$.
故答案为:$\sqrt{6}$-$\sqrt{2}$.
点评 本题考查直线与圆的位置关系,考查弦长的计算,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:填空题
 如图,已知|$\overrightarrow{OA}$|=2,|$\overrightarrow{OB}$|=2$\sqrt{3}$,$\overrightarrow{OA}$•$\overrightarrow{OB}$=0点C在线段AB上,∠AOC=30°,用$\overrightarrow{OA}$和$\overrightarrow{OB}$来表示向量$\overrightarrow{OC}$,则$\overrightarrow{OC}$等于$\frac{3}{4}\overrightarrow{OA}$+$\frac{1}{4}\overrightarrow{OB}$.
如图,已知|$\overrightarrow{OA}$|=2,|$\overrightarrow{OB}$|=2$\sqrt{3}$,$\overrightarrow{OA}$•$\overrightarrow{OB}$=0点C在线段AB上,∠AOC=30°,用$\overrightarrow{OA}$和$\overrightarrow{OB}$来表示向量$\overrightarrow{OC}$,则$\overrightarrow{OC}$等于$\frac{3}{4}\overrightarrow{OA}$+$\frac{1}{4}\overrightarrow{OB}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
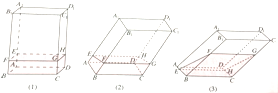 如图,透明塑料制成的长方体ABCD-A′B′C′D内灌进一些水,固定容器底面一边BC与地面上,再将容器倾斜.随着倾斜度的不同,有下面四个命题:
如图,透明塑料制成的长方体ABCD-A′B′C′D内灌进一些水,固定容器底面一边BC与地面上,再将容器倾斜.随着倾斜度的不同,有下面四个命题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | PD?平面ABC | B. | PD⊥平面ABC | ||
| C. | PD与平面ABC相交但不垂直 | D. | PD∥平面ABC |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{2}{9}$,$\frac{1}{4}$) | B. | [$\frac{2}{9}$,$\frac{1}{4}$] | C. | (0,$\frac{2}{9}$] | D. | (0,$\frac{1}{4}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com