
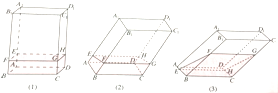
 如图,透明塑料制成的长方体ABCD-A′B′C′D内灌进一些水,固定容器底面一边BC与地面上,再将容器倾斜.随着倾斜度的不同,有下面四个命题:
如图,透明塑料制成的长方体ABCD-A′B′C′D内灌进一些水,固定容器底面一边BC与地面上,再将容器倾斜.随着倾斜度的不同,有下面四个命题:分析 利用棱柱的结构特征及柱体的体积公式逐一核对四个选项得答案.
解答 解:①在以BC为旋转轴倾斜的过程中,平面ABFE∥平面DCGH,其余的面为四边形,且相邻四边形的公共边互相平行,故有水的部分始终呈棱柱形,没水的部分也始终呈棱柱形,①正确;
②∵A′D′∥EH,∴棱A′D′始终与水面所在平面平行,②正确;
③水面EFGH中FG为定值,EF变化,则水面EFGH所在四边形的面积变化,③错误;
④∵容器中水的容积为定值,且棱柱BEF-CHG的高BC为定值,∴当容器倾斜如图3所示时,BE•BF是定值,④正确.
∴正确命题的序号是①②④.
故答案为:①②④.
点评 本题考查棱柱的结构特征,考查了棱柱的体积,考查空间想象能力和思维能力,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设点P为圆C1:x2+y2=2上的动点,过点P作x轴的垂线,垂足为Q,点M满足$\sqrt{2}$$\overrightarrow{MQ}$=$\overrightarrow{PQ}$.
设点P为圆C1:x2+y2=2上的动点,过点P作x轴的垂线,垂足为Q,点M满足$\sqrt{2}$$\overrightarrow{MQ}$=$\overrightarrow{PQ}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com