
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 由①可得f(x)+f(2-x)=0,求得x在[1,3]上的f(x)的解析式;再由②求得x在[-3,-1]上的解析式,画出f(x)和y═($\frac{1}{2}$)|x|在[-3,3]的图象,通过图象观察,可得它们有5个交点,即可得到零点的个数.
解答 解:由题意可得f(x)+f(2-x)=0,
当1≤x≤2时,0≤2-x≤1,f(2-x)=cos$\frac{π}{2}$(2-x)=-cos$\frac{π}{2}$x,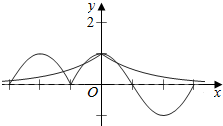
则f(x)=-f(2-x)=cos$\frac{π}{2}$x;
当2<x≤3时,-1≤x<0,f(2-x)=1-(2-x)2,
则f(x)=-f(2-x)=(2-x)2-1.
由②f(-1+x)=f(-1-x),即为f(x)=f(-x-2),
当-3≤x≤-2时,0≤-2-x≤1,f(-2-x)=cos$\frac{π}{2}$(-2-x)=-cos$\frac{π}{2}$x,
则f(x)=-f(-2-x)=-cos$\frac{π}{2}$x;
当-2<x≤-1时,-1≤-2-x<0,f(-2-x)=1-(-2-x)2,
则f(x)=f(-2-x)=1-(-2-x)2.
y=f(x)-($\frac{1}{2}$)|x|在区间[-3,3]上的零点
即为y=f(x)和y=($\frac{1}{2}$)|x|在[-3,3]的交点个数.
作出y=f(x)和y═($\frac{1}{2}$)|x|在[-3,3]的图象,
通过图象观察,可得它们有5个交点,
即有5个零点.
故选:C.
点评 本题考查函数的性质和运用,考查函数方程的转化思想,注意运用数形结合的思想方法,属于中档题.


 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案科目:高中数学 来源: 题型:填空题
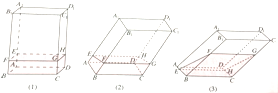 如图,透明塑料制成的长方体ABCD-A′B′C′D内灌进一些水,固定容器底面一边BC与地面上,再将容器倾斜.随着倾斜度的不同,有下面四个命题:
如图,透明塑料制成的长方体ABCD-A′B′C′D内灌进一些水,固定容器底面一边BC与地面上,再将容器倾斜.随着倾斜度的不同,有下面四个命题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{4}{7}$ | D. | $\frac{6}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x1)<0,f(x2)<0 | B. | f(x1)>0,f(x2)>0 | C. | f(x1)>0,f(x2)<0 | D. | f(x1)<0,f(x2)>0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com