
分析 (1)化直线系方程为m(2x+y-7)+x-y+1=0,联立$\left\{\begin{array}{l}{2x+y-7=0}\\{x-y+1=0}\end{array}\right.$求得直线所过定点坐标,代入圆的方程验证得答案;
(2)化圆的一般方程为标准方程,求出圆心坐标和半径,画图可得当直线与CM垂直时,直线l与圆C所截得的弦长的最短,由垂径定理求得弦长,再由直线方程的点斜式求得直线方程.
解答 证明:(1)化直线l:(2m+1)x+(m-1)y=7m-1为m(2x+y-7)+x-y+1=0,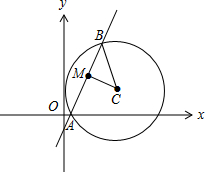
联立$\left\{\begin{array}{l}{2x+y-7=0}\\{x-y+1=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=2}\\{y=3}\end{array}\right.$,
∴直线l过定点(2,3),
∵22+32-8×2-4×3+4=-11<0,
∴点(2,3)在圆C内部,则不论m取什么实数,直线l与圆C一定相交;
解:(2)化圆C:x2+y2-8x-4y+4=0为(x-4)2+(y-2)2=16,
圆心坐标C(4,2),圆的半径r=4,
如图,直线l过定点M(2,3),
当直线l垂直于CM时,直线l被圆解得的弦长最短,
∵|CM|=$\sqrt{(4-2)^{2}+(2-3)^{2}}=\sqrt{5}$,r=4,
∴弦|AB|=$2\sqrt{{4}^{2}-(\sqrt{5})^{2}}=2\sqrt{11}$.
${k}_{CM}=\frac{3-2}{2-4}=-\frac{1}{2}$,
∴所求直线方程为y-3=2(x-2),即2x-y-1=0.
点评 本题考查直线与圆的位置关系,考查了直线系方程的应用,训练了利用垂径定理求弦长,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 3 | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
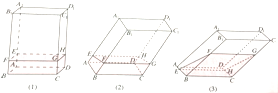 如图,透明塑料制成的长方体ABCD-A′B′C′D内灌进一些水,固定容器底面一边BC与地面上,再将容器倾斜.随着倾斜度的不同,有下面四个命题:
如图,透明塑料制成的长方体ABCD-A′B′C′D内灌进一些水,固定容器底面一边BC与地面上,再将容器倾斜.随着倾斜度的不同,有下面四个命题:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C的中心在原点,焦点在x轴上,离心率为$\frac{\sqrt{2}}{2}$,过椭圆C上一点P(2,1)作x轴的垂线,垂足为Q.
已知椭圆C的中心在原点,焦点在x轴上,离心率为$\frac{\sqrt{2}}{2}$,过椭圆C上一点P(2,1)作x轴的垂线,垂足为Q.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | PD?平面ABC | B. | PD⊥平面ABC | ||
| C. | PD与平面ABC相交但不垂直 | D. | PD∥平面ABC |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com